Fibonacci
Let be the th Fibonacci number ( , where and . Find the smallest such that . Give as the answer.
Bonus: How many digits this has?
The answer is 750.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solution with Java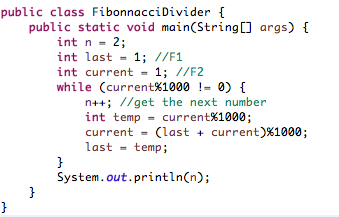
java public class FibonnacciDivider { public static void main(String[] args) { int n = 2; int last = 1; //F1 int current = 1; //F2 while (current%1000 != 0) { n++; //get the next number int temp = current%1000; current = (last + current)%1000; last = temp; } System.out.println(n); } }(how do I fix the text... until then just take this)