Fibonacci

We will prove that $a_1^2+a_2^2+a_3^2+a_4^2+\dots +a_{n-1}^2+a_n^2=a_n*a_{n+1}$ where $a_k$ is the $k.$ item of the Fibonacci sequence. We will use Full induction. If $n=1$ , then $1=1*1$ . Suppose for $n=x$ the statement is true. We will prove that the statement is also true for $n=x+1$ : Since $a_1^2+a_2^2+\dots +a_x^2=a_x*a_{x+1}$ , $a_1^2+a_2^2+\dots +a_x^2+a_{x+1}^2=a_x*a_{x+1}+a_{x+1}*a_{x+1}=a_{x+1}*(a_x+a_{x+1})=a_{x+1}*a_{x+2}$

Now we proved the statement.

The $n+2$ . item of the sequence is $1597+2854=4451$ , so $1^2+1^2+2^2+3^2+\dots +1597^2+2854^2=2854*4451=\boxed{12703154}.$

A nice representation mode for the solution ( $for n=5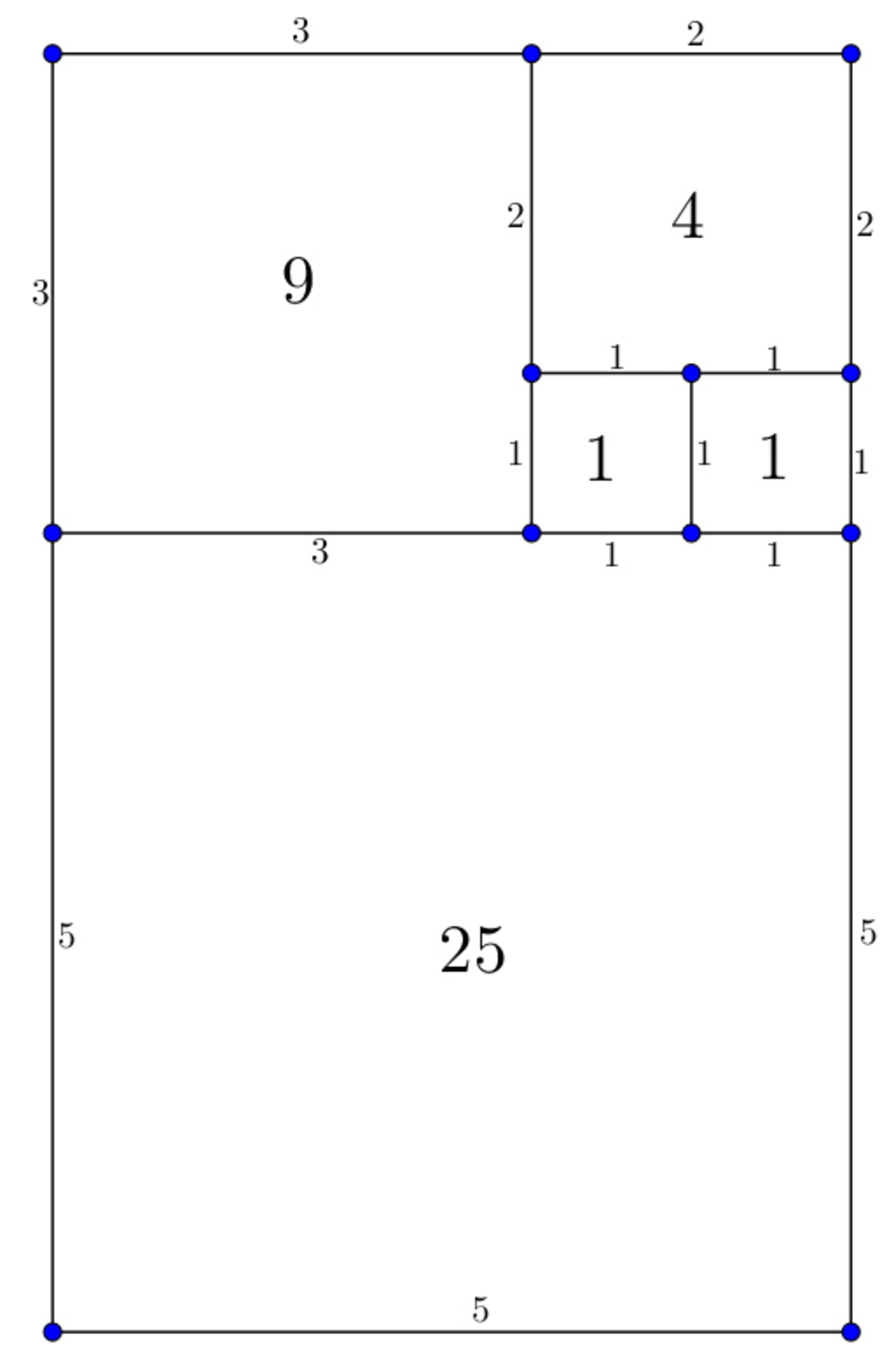$ ): The rectangle's area is $a_{n+1}*a_{n+2}$ .