Fibonacci Bins

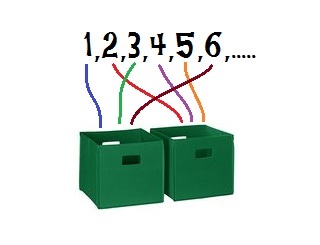
The numbers 1 through $n$ (inclusive) are separated into 2 bins.

For each bin, no two different numbers in it can add up to a Fibonacci number .

The Fibonacci numbers are given by:

$1,1,2,3,5,8,13,21....$

And in general they satisfy the following recursion relation:

• $F(0) = F(1) = 1$
• $F(n) = F(n-2) + F(n-1)$ for $n > 1$

What is the largest $n$ for which this is possible?

If you think the answer is infinite, please put 99999 as your answer.

---

Image credit: http://www.shopstyle.com/