Fibonacci Circles
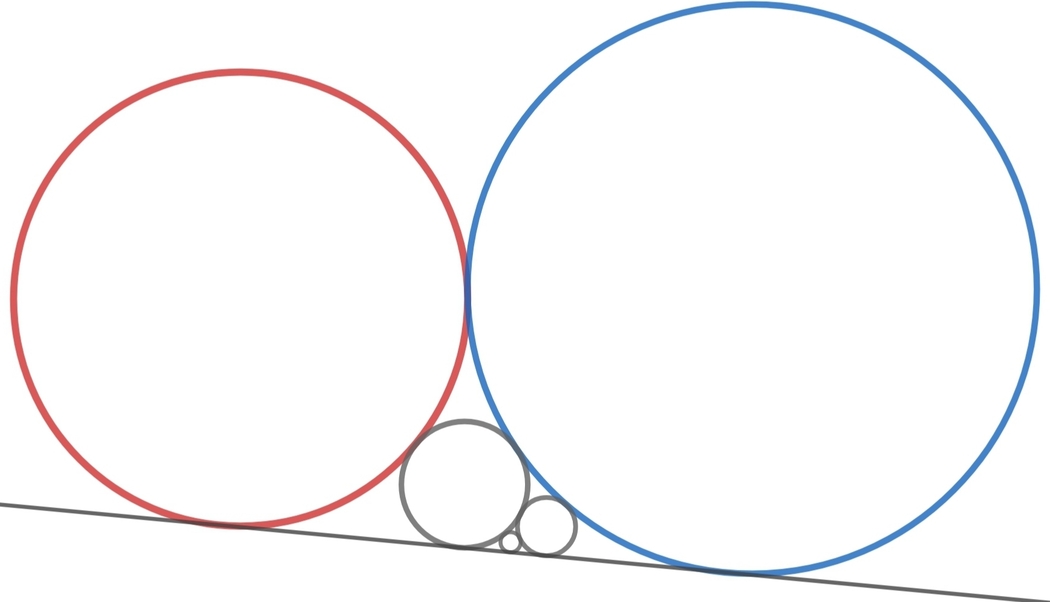
Consider two circles C 1 and C 2 tangent to each other and also to a line L at points T 1 and T 2 .
We draw a chain of circles C 3 , C 4 , C 5 , ⋯ such that C n is tangent to C n − 1 , C n − 2 and the line L .
This sequence of circles approaches a limiting point T ∞ on the line L .
If T ∞ divides the segment T 1 T 2 into equal parts, then find the ratio of the radius of C 1 to the radius of C 2 .
Notation: φ = 2 1 + 5 denotes the golden ratio .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Digvijay Singh , I finally got it.
Let radii of C 1 , C 2 be r 1 , r 2 . Then
φ 2 = r 1 r 2 = φ + 1
How did you arrive at this?
When I get the time.
Let the red circle be C 1 , the blue circle be C 2 , radius of C n be r n , and the length T j T k = ℓ j k .
Then ℓ 1 2 = ( r 1 + r 2 ) 2 − ( r 1 − r 2 ) 2 = 2 r 1 r 2 and ℓ 1 3 + ℓ 2 3 = ℓ 1 2 ⟹ 2 r 1 r 3 + 2 r 2 r 3 = 2 r 1 r 2 ⟹ r 3 = r 1 + r 2 r 1 r 2 . Putting r 1 = 1 and r 2 = x , we have:
r 3 r 4 r 5 ⟹ r n = r 1 + r 2 r 1 r 2 = 1 + x x = r 2 + r 3 r 2 r 3 = 2 + x x = r 3 + r 4 r 3 r 4 = 3 + 2 x x = r n − 2 − r n − 1 r n − 2 r n − 1 = F n − 3 + F n − 4 x x + F n − 2 + F n − 3 x x F n − 3 + F n − 4 x x × F n − 2 + F n − 3 x x = F n − 1 + F n − 2 x x By proof by induction where F k is the k th Fibonacci number.
Let the distance of T n from T 1 be d n and to simplify, ℓ n = ℓ n , n + 1 , then
d 1 d 2 d 3 d 4 d 5 ⟹ d n = ℓ 1 = 2 r 1 r 2 = 2 x = ℓ 1 − ℓ 2 = 2 x ( 1 − 1 + x x ) = 1 + x 2 x = ℓ 1 − ℓ 2 + ℓ 3 = 1 + x 2 x ( 1 + 2 + x x ) = 2 + x 4 x = 2 + x 2 x ( 2 − 3 + 2 x x ) = 3 + 2 x 6 x = 3 + 2 x 2 x ( 3 + 5 + 3 x x ) = 5 + 3 x 1 0 x = F n − 1 + F n − 2 x 2 F n − 1 x By induction
Since d ∞ = 2 ℓ 1 = x ,
x φ x + x 2 ⟹ x = n → ∞ lim F n − 1 + F n − 2 x 2 F n − 1 x = n → ∞ lim F n − 2 F n − 1 + x 2 x × F n − 2 F n − 1 = φ + x 2 φ x = 2 φ x = φ Divide up and down by F n − 2 Note that n → ∞ lim F n F n + 1 = φ , the golden ratio
Note that x = r 1 r 2 , therefore r 2 r 1 = x 2 1 = φ 2 1 = φ + 1 1 .