Fibonacci Divisibility Graph
Let be the sequence of Fibonacci numbers ; that is, and for all .
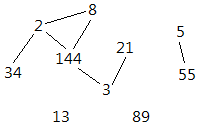
Consider a graph with vertices labeled , and two (different) vertices are connected by an edge if and only if or . The above picture is the graph for .
Find the largest such that this graph is planar. If there is no largest , enter .
The answer is 29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The answer is 29.
First, the Fibonacci numbers have the property that F a ∣ F b if and only if a ∣ b . Thus, we can construct a graph with 3 , 4 , 5 , … , N instead of F 3 , F 4 , F 5 , … , F N , apply the same divisibility rule (an edge if a vertex is multiple of the other), and obtain an isomorphic graph.
With this, the following is a planar embedding for N = 2 9 , with labels 3 , 4 , … , N instead of F 3 , F 4 , … , F N :
Now, showing that N ≥ 3 0 is impossible is actually simpler. By Kuratowski's theorem , a graph is not planar if and only if there exists a subgraph of it isomorphic to a subdivision of either K 5 or K 3 , 3 . We claim there exists a subgraph isomorphic to a subdivision of K 3 , 3 . This is best shown by a picture:
Thus no N ≥ 3 0 will make it planar (because it will contain the above subgraph), so the largest N is 2 9 .