Fibonacci Multiples of Nine

If we write out the first 24 terms of the Fibonacci sequence mod 9, we get $1, 1, 2, 3, 5, 8, -5, 3, -2, 1, -1, 0,$ $-1, -1, -2, -3, -5, -8, 5, -3, 2, -1, 1, 0$ . Then the 25th and 26th terms are 1 again. Since each term only depend on the two previous terms, $(F_1, F_2)=(F_{25}, F_{26})$ , which tells us that the Fibonacci sequence has a period of 24 in modulo 9. Since out of the first 24 terms, two multiples of 9 occur on the 12th and the 24th, we may conclude that $F_n$ is a multiple of 9 whenever $n=24k+12$ or $n=24k$ , where $k$ is a nonnegative integer. Thus there are $\lfloor \frac{1000}{12} \rfloor=\boxed{83}$ total number of multiples of 9.

The Fibonacci sequences are 1,1,2,3,5,8,13,21,34,55,89,144,.. When this sequences is divided by 9, its sequences remainder is 1,1,2,3,5,8,4,3,7,1,8,0,8,8,7,6,4,1,5,6,2,8,1,0,1,1,2,3,5,8,4,3,7,1,8,0,... Every twelve continuously term of sequence, we have one divisible by 9. 1000= 12*83 + 4 Therefore, there are 83 terms of the first 1000 terms are multiples of 9

We write the sequence in modulo 9, so it would be 1,1,2,3,5,8,4,3,7,1,8,0,8,8,7,6,4,1,5,6,2,8,1,0,1,1,2,3,... We note that the sequence is periodic in 24 terms, at which we only need to note that every other 12th term there will be a number divisible by 9. So as 1000=83*12+4. There will be 83 numbers in the sequence that is divisible by 9.

Rather than looking at the numbers themselves, look at the remainders when divided by 9.

the cycle goes 1,1,2,3,5,8,4,3,7,1,8,0 ,8,8,...

Now 8 is the same as -1 mod 9

so after 12 numbers we now have a sequence that starts -1,-1,.... this will be the same as the above except with negative signs.

So every 12th fibonacci number is a multiple of 9. There are 83 full cycles of 12 in 1000, so there are 83 multiples of 9

We first find out the first 26 terms modulo 9: 1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 0, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 0, 1, 1. It can be easily seen the pattern repeats. Note that $F_{12}$ and $F_{24}$ are divisible by 9. It can be concluded easily that $F_n$ where 12 is a factor of n, is divisible by 9. Thus, there are $\lfloor\frac{1000}{12}\rfloor=83$ multiples of 9.

To work this out, we can observe a pattern that every 12 integers, there will be a multiple of 9. Thus, 1000/12 is approximately 83.

I can't find a non-messier way but,

Taking the Fibonacci Sequence modulo 9,

$1,1,2,3,5,8,4,3,7,1,8,0,8,8,7,6,4,1,5,6,2,8,1,0,1,1, \ldots$

We see that the sequence restarts after every 24 terms and 0 appears every 12th term.

Therefore number of $0$ s i.e. number of terms divisble by 9 in the first 1000 terms are $\lfloor \frac{1000}{12} \rfloor$

which is equal to $\boxed{83}$

According to the wikipedia article about Fibonacci numbers, 'every kth number of the sequence is a multiple of Fk'. But then, if you're lazy like me, and especially if you know that you can't count reliably (and I mean this seriously), you do something like this.

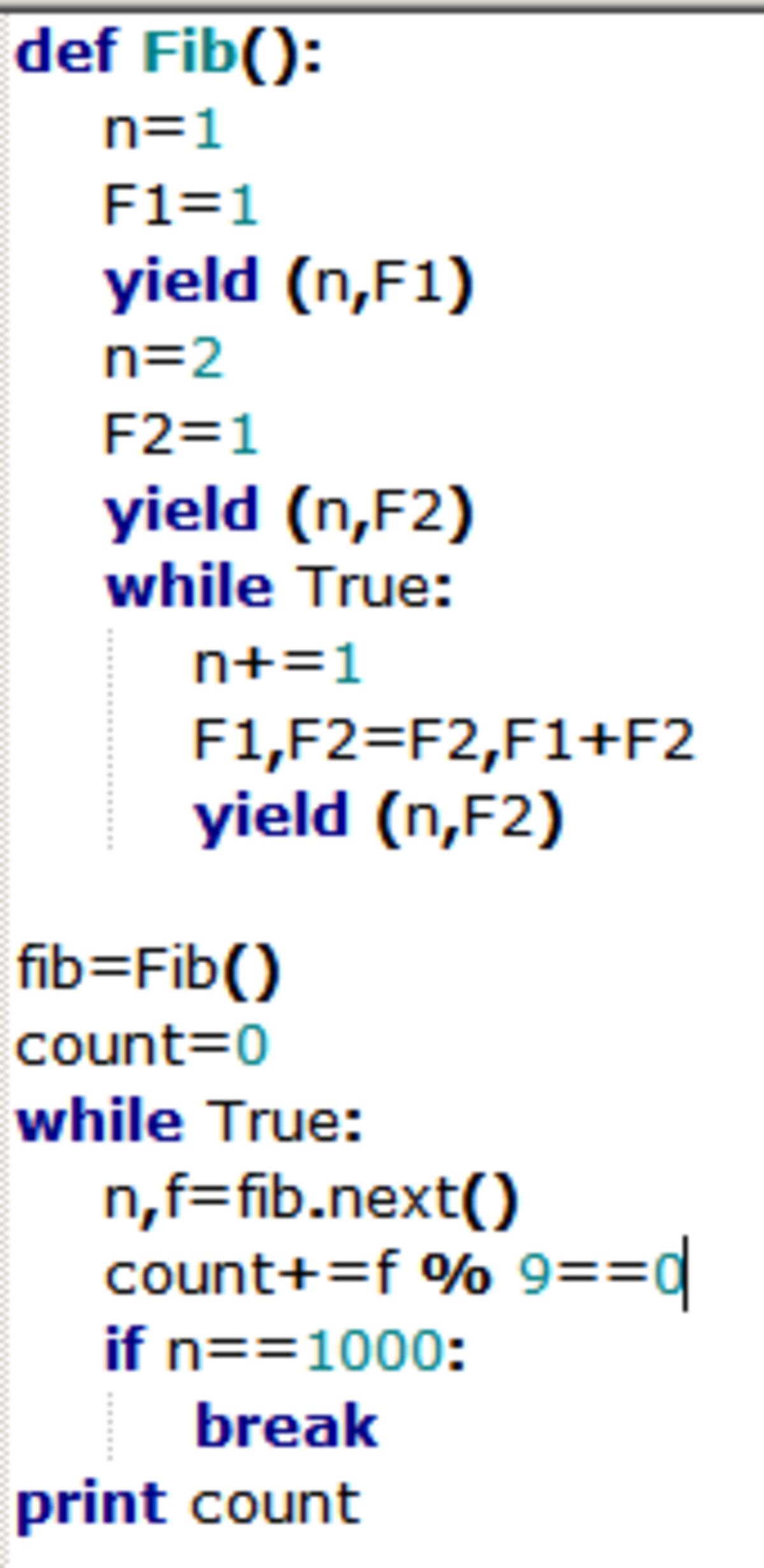
Incidentally, the wikipedia article appears to reference works that demonstrate the truth of the property of Fibonacci sequences that others have been using here.

Consider the first few numbers of the Fibonacci sequence modulo 3. We have: 1, 1, 2, 0, 2, 2, 1, 0, etc., corresponding to 1, 1, 2, 3, 5, 8, 13, 21, etc. Note that, for example, 2+2 (modulo 3) = 1 (modulo 3), which equals 13 (modulo 3). Thus we can continue to add terms in the Fibonacci sequence modulo 3 as we would in normal arithmetic.

Continuing to write out these terms' remainders when dividing by 3 shows a repeating pattern: 1, 1, 2, 0, 2, 2, 1, 0, 1, 1... After the 8th term, the sequence restarts with 1, 1, ..., showing that every 8 terms are identical modulo 3. Thus, every 4th term is divisible by 3.

Since 9 = 3*3, it is not too difficult to prove that every 12th term will then be divisible by 9. Thus, the desired answer is (floor of 1000/12) = 83.