Fibonacci numbers out of the blue

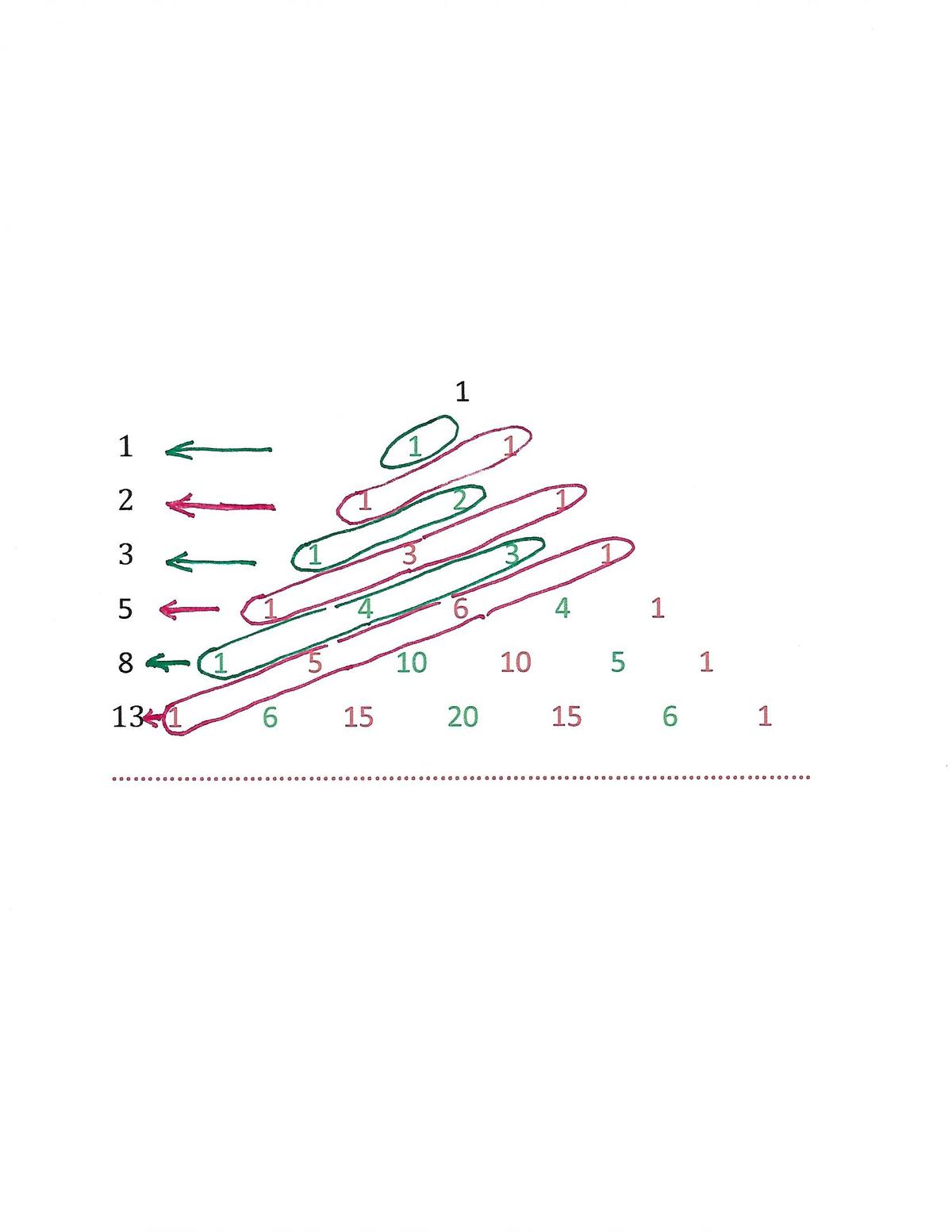
Here's a "visual" induction proof that the sum of the terms in the $n$ th "gentle" (couldn't think of a better antonym for 'steep') diagonal of Pascal's triangle is $F_n$ , the $n$ th Fibonacci number.

Here the terms in diagonal $D_n$ correspond to the terms in the sum $\displaystyle \sum_{k = 0}^{ \big\lfloor \frac{n}{2} \big\rfloor } \small \dbinom{n-k}{k}$ .

Basis: Sum of terms in $D_0$ is ${\small \dbinom{0}{0}} = 1 = F_0$ ; sum of terms in $D_1$ is ${\small \dbinom{1}{0}} = 1 = F_1$ .

Induction: Suppose the sum of the terms in $D_{n - 2}$ is $F_{n - 2}$ and the sum of the terms in $D_{n - 1}$ is $F_{n - 1}$ . Every term in $D_n$ is the sum of the two terms above it in the same color, one in $D_{n - 1}$ , the other in $D_{n - 2}$ . Then the sum of the terms in $D_n$ is the sum of the terms in both $D_{n - 1}$ and $D_{n - 2}$ , i.e. the sum of the terms in $D_n$ is $F_{n - 2} + F_{n - 1} = F_n$ .

For any number n the sum is the (n+1) st Fibonacci number. By the way the binomial coefficients in the sum can be found in the Pascal's triangle as shown bellow.