Fibonacci Puzzle
 Find the smallest Fibonacci number which contains all digits (
0
−
9
).
Find the smallest Fibonacci number which contains all digits (
0
−
9
).
Note: The digits may be repeated.
The answer is 2504730781961.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
+1 for generator functions and sets! :)
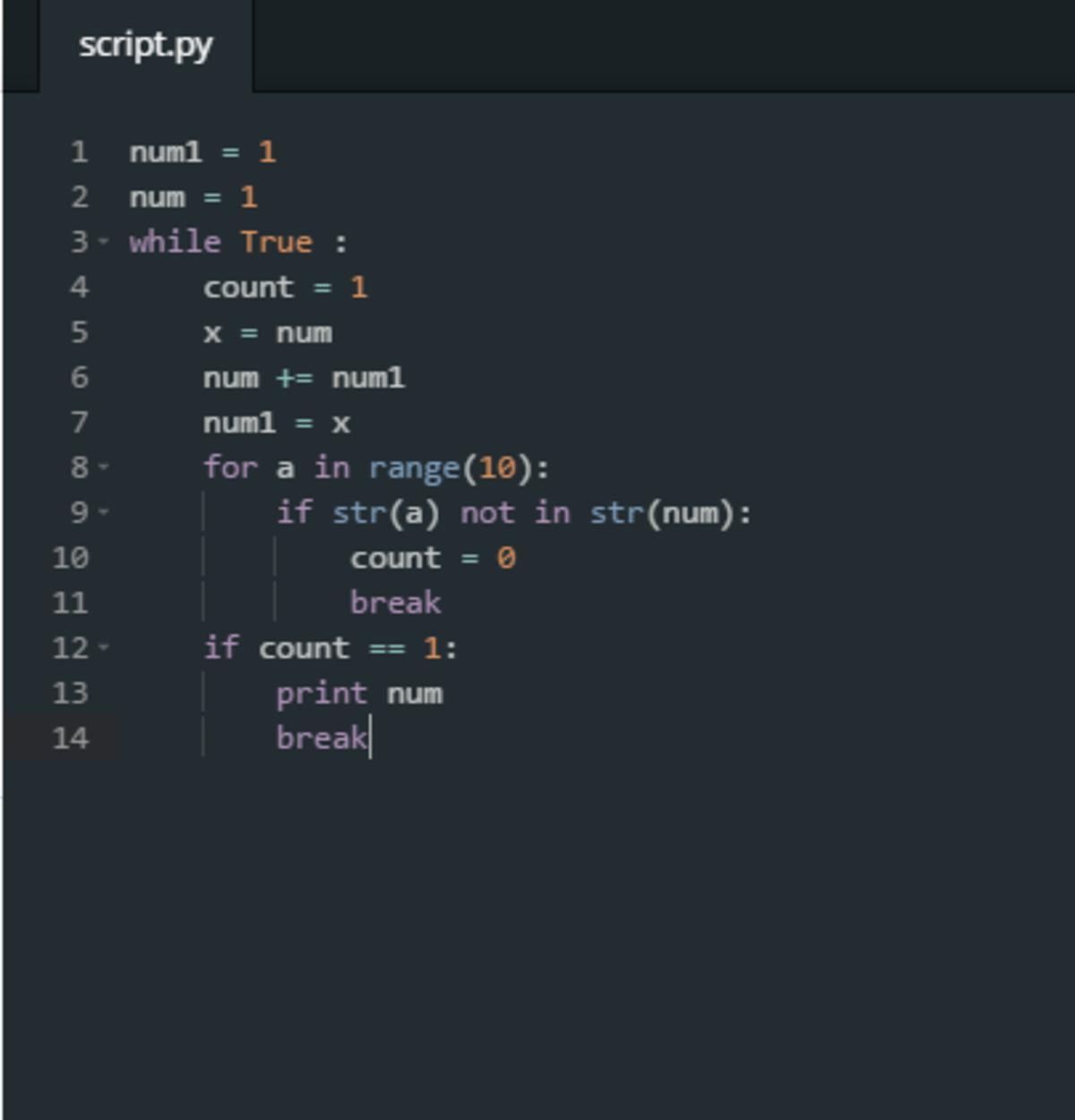
Python 2.7:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
|
Nice! My method was little different.
Nice!! Python!! Impressive.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
|
Execution time ~ 0.08 seconds
What? You guys used codes to calculate all this, I constructed the whole fibbonnacci table till 100 digits and then found the answer
What..... you did so much donkey's work :P lol