Field Cancellation
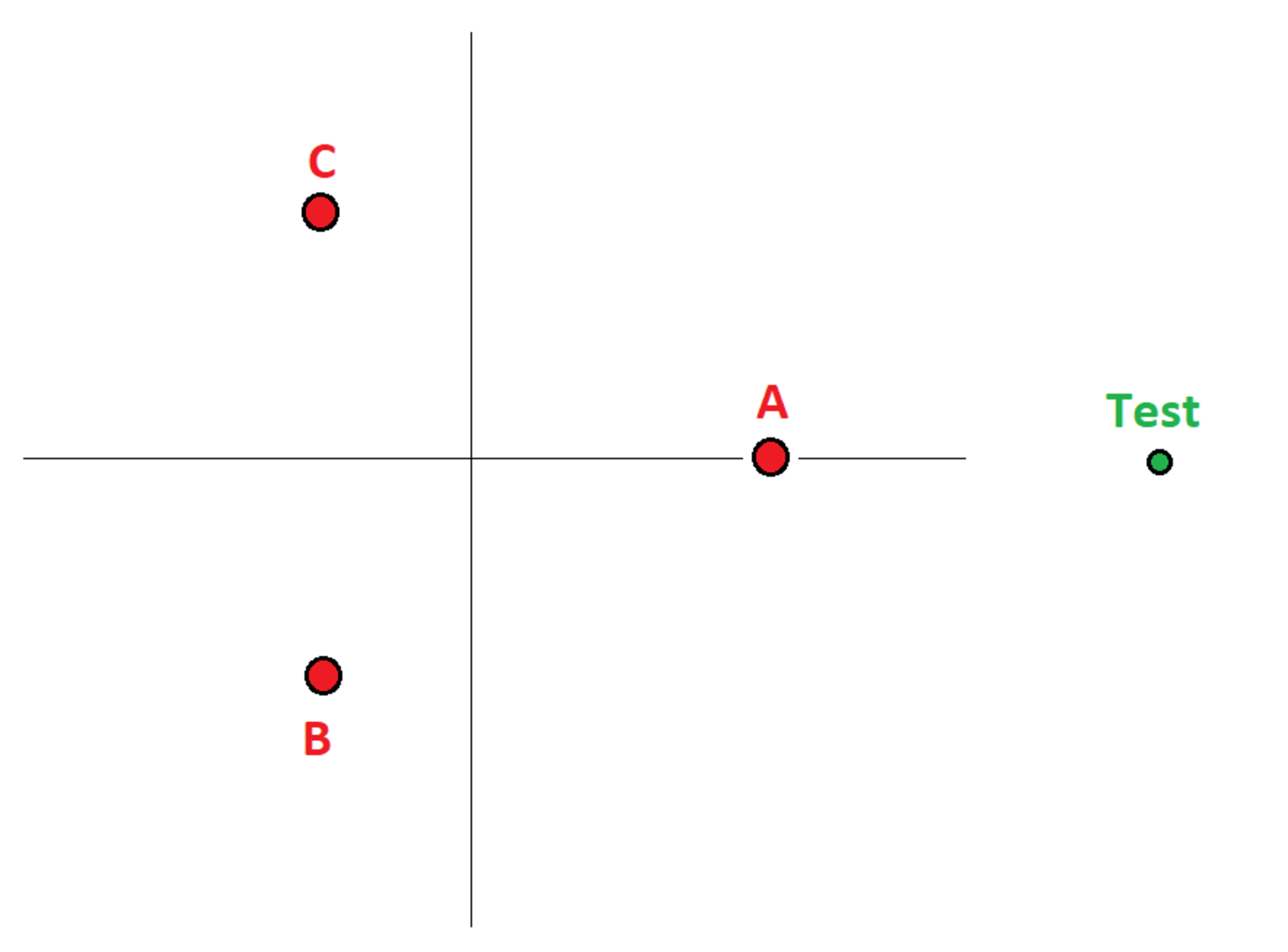
There are three infinitely long straight wires named A , B , and C . They are perpendicular to the x y plane, and they have the following coordinates in the x y plane:
( x A , y A ) = ( 1 , 0 ) ( x B , y B ) = ( − 2 1 , − 2 3 ) ( x C , y C ) = ( − 2 1 , 2 3 )
There is a test point in the x y plane at position ( x T , 0 ) . In "Scenario 0", the wires carry the following constant currents:
I A 0 = 1 I B 0 = 1 I C 0 = 1
In "Scenario 1", the wires carry the following constant currents:
I A 1 = 1 I B 1 = − 2 1 I C 1 = − 2 1
Let B 0 ( x T ) be the magnitude of the net magnetic field at the test point in Scenario 0, and let B 1 ( x T ) be the magnitude of the net magnetic field at the test point in Scenario 1. The field values vary as x T changes.
Determine the following integral:
∫ 1 . 1 3 0 ( B 0 ( x T ) B 1 ( x T ) ) d x T
Bonus: Make a plot of the ratio as a function of x T and comment on the physical interpretation of the result
Note: I named the scenarios "0" and "1" because in three-phase AC power, the common mode is known as the "zero sequence", whereas the "positive sequence" quantities are separated by 1 2 0 electrical degrees. The positive sequence is associated with the number "1".
The answer is 2.091.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Total induction of magnetic field at ( x T , 0 ) due to the three currents is B t o t = 2 π μ 0 × ( x T − 1 I A + 2 x T 2 + 2 x T + 2 I B × ( 2 x T + 1 ) + 2 x T 2 + 2 x T + 2 I C × ( 2 x T + 1 ) ) . In the first case, I A 0 = I B 0 = I C 0 = 1 and so B 0 ( x T ) = 2 π μ 0 × x T 3 − 1 3 x T 2 , while in the second case, I A 1 = 1 , I B 1 = I C 1 = − 2 1 . So, B 1 ( x T ) = 2 π μ 0 × 2 x T 3 − 2 3 x T + 3 . Therefore B 0 ( x T ) B 1 ( x T ) = 2 x T 1 + 2 x T 2 1 , and the value of the given integral is 2 ln 1 . 1 3 0 + 2 1 ( 1 . 1 1 − 3 0 1 ) = 2 . 0 9 0 8 . . . .
The formula for the magnetic field due to an infinite wire is:
B = 2 π ∣ a ∣ μ o I ( d l × a ^ )
Where a is the vector joining the wire and the test point and directed towards the test point and d l is in the direction of current flow in the wire.
Let the coordinates of the test point be ( x , 0 ) .
Applying this to the scenario '0' gives a net field in the negative Y direction and the magnitude of the field is:
B T o = 2 π ( x − 1 ) μ o I A o + 2 π ( ( x + 0 . 5 ) 2 + ( − 3 / 2 ) 2 ) μ o I B o ( x + 0 . 5 ) + 2 π ( ( x + 0 . 5 ) 2 + ( 3 / 2 ) 2 ) μ o I C o ( x + 0 . 5 )
Doing the same for scenario '1' gives the net field again along the Y direction. The field due to wire A is along negative Y while that due to B and C is along the positive Y direction:
B T 1 = 2 π ( x − 1 ) μ o I A 1 + 2 π ( ( x + 0 . 5 ) 2 + ( − 3 / 2 ) 2 ) μ o I B 1 ( x + 0 . 5 ) + 2 π ( ( x + 0 . 5 ) 2 + ( 3 / 2 ) 2 ) μ o I C 1 ( x + 0 . 5 )
The fields along X in both scenarios cancel out. Having obtained the fields, the next step is to evaluate the ratio:
B T o B T 1 = R = 2 x 2 x + 1
The simplification carried out to obtain the above expression is left out. From this point, the integral is trivial to evaluate:
I = ∫ 1 . 1 3 0 R d x = 2 ln ( 3 0 ) − ln ( 1 0 1 1 ) + 3 3 0 2 8 9 ≈ 2 . 0 9 0 8
It can be seen that as x increases, the ratio reduces, which indicates that the field in scenario 1 reduces in magnitude relative to that in scenario 0. The field in scenario 1 tends towards cancellation as x increases.