Figuring out the pattern
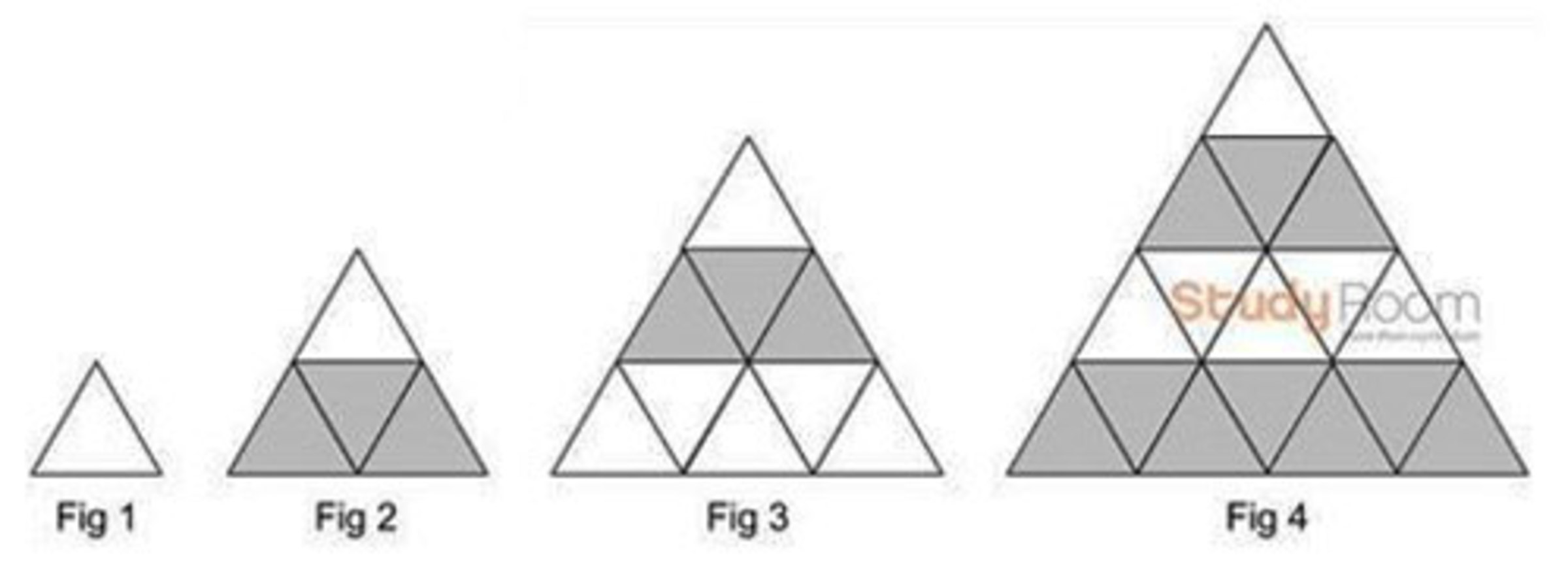
The series of figures above follow a certain pattern, find the percentage (%) of grey triangles to all triangles in Fig 250 .
The answer is 50.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The number of all triangles in Fig n is given by:
S t ( n ) = k = 1 ∑ n ( 2 k − 1 ) = 2 ⋅ 2 n ( n + 1 ) − n = n 2
The number of grey triangles in FIg n , where n is even, is given by:
S g ( n ) = k = 1 ∑ 2 n ( 4 k − 1 ) = 2 4 ( 2 n ( 2 n + 1 ) ) − n = 2 n ( n + 1 )
⟹ S t ( n ) S g ( n ) S t ( 2 5 0 ) S g ( 2 5 0 ) = 2 n 2 n ( n + 1 ) = 2 n n + 1 = 5 0 0 2 5 1 = 5 0 . 2 %
Wow I did the same but must have made an error. I kept getting 50.7 :(
Fig. 2 has 3 gray triangles on 2² = 4
Fig. 4 has 3 + 3 + 4 = 3 + 7 = 10 gray triangles on 4² = 16
Fig. 6 would have 3 + 7 + 7 + 4 = 3 + 7 + 11 = 21 gray triangles on 6² = 36
...
It seem that if fig. n (n is even) has 2 n 2 + 2 n gray triangles on n 2 or in percentage 5 0 ( 1 + n 1 ) % than in fig. (n+2) there are 2 n 2 + 2 n + 2 n + 3 = 2 1 ( n 2 + 5 n + 6 ) = 2 ( n + 2 ) 2 + 2 ( n + 2 ) gray triangles on ( n + 2 ) 2 or in percentage 5 0 ( 1 + n + 2 1 )
So it's demonstrated by induction that in fig. n (n even) there are 2 n 2 + 2 n gray triangles on n² or in percentage 5 0 ( 1 + n 1 ) %
In particular for n= 250 percentage is 5 0 ( 1 + 2 5 0 1 ) = 5 0 , 2 %
As shown on Fig 4 below, the following transformations can be completed on any even figure and still preserve the percentage of gray triangles to all triangles. (The white triangles were changed to blue triangles to distinguish them from the white background.)
In general, for each even Fig n , there are 2 1 n 2 + 2 1 n gray squares and a total of n 2 squares, for a ratio of 2 n 2 n 2 + n .
Therefore, Fig 2 5 0 will be 2 ⋅ 2 5 0 2 2 5 0 2 + 2 5 0 ⋅ 1 0 0 = 5 0 . 2 % gray.