Fill a 5×5 grid!

Each row can be filled in one of $13$ different ways, each way representing one of the binary numbers in $S = \{0, 1, 2, 4, 8, 16, 5, 9, 10, 17, 18, 20, 21\}$ .

If a particular row is represented by the number $x \in S$ , then then next row can be represented by the number $y \in S$ provided that the bitwise AND $x \mathrm{\&} y$ of $x$ and $y$ is $0$ . Thus we can obtain the recursive formulae $\begin{aligned} X_0(x) & = \; 1 \\ X_m(x) & = \; \sum_{y \in S,x \mathrm{\&} y = 0}X_{m-1}(y) \end{aligned} \hspace{3cm} x \in S\,,\, m \ge 1$ where $X_m(x)$ is the number of ways in which an $(m+1) \times 5$ array can be filled with no adjacent $1$ s, given that the first row is represented by the number $x \in S$ . It is a simple matter to calculate that $X_5(0) \; = \; \boxed{55447}$

Another way of seeing this result is to note that the first, third and fifth rows can be chosen freely from $S$ . If the first, third and fifth rows are $x,y,z \in S$ respectively, then the second row could be any $u \in S$ such that $u \mathrm{\&} x = u \mathrm{\&} y = 0$ , and hence such that $u \mathrm{\&} (x|y) = 0$ , where $x|y$ is the bitwise OR of $x$ and $y$ . If we define $N(x,y) \; = \; \left| \big\{ u \in S \,\big| \, u \mathrm{\&} (x|y) = 0\big\} \right| \hspace{2cm} x,y \in S$ then the desired number of grid numberings is $\sum_{x,y,z \in S} N(x,y)N(y,z) \; = \; \sum_{y \in S} \left(\sum_{x \in S} N(x,y)\right)^2 \; = \; 55447$

This is an example of a $5×5$ grid:

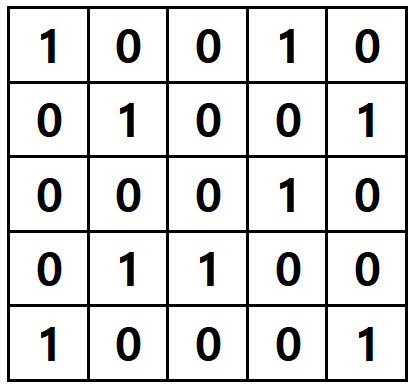
You can make a C - programme to solve this problem. (If you run the programme and type "5 5" and wait for just a few seconds, you can get the answer.)

Try it!!!

The condition is equivalent to stating that no two ones can be adjacent. Focusing on rows, there are 13 different rows possible: A=00000, B=00001, C=00010, D=00100, E=00101, F=01000, G=01001, H=01010, I=10000, J=10001, K=10010, L=10100, M=10101.

Two rows can occur directly above each other if they have no ones in common (for the programmers: a bitwise logical AND should result in 0).

Pattern A can have all 13 neighbours (ABCDEFGHIJKLM) directly below or above it, B can have 8 (ACDFHIKL), C can have 10 (ABDEFGIJLM), D can have 9 (ABCFGHIJK), E can have 6 (ACFHIK), F can have  10 (ABCDEIJKLM), G can have 6 (ACDIKL), H can have 8 (ABDEIJLM), I can have 8 (ABCDEFGH), J can have 5 (ACDFH), K can have 6 (ABDEFG), L can have 6 (ABCFGH), M can have 4 (ACFH).

We start filling the grid by choosing a pattern for the middle row

• suppose it is an A-pattern. above that row, we can have any row, suppose that row is a C then it can have 10 neigbours. It can be any of the others too, so A in  the middle gives 13+10+...+4=99 ways to put 2 rows above it and also 99 ways to put two rows below it $99^2$ .
• suppose it is a B-pattern. Next to row B we can have A,C,D,F,... so certain neighbours are excluded. The rows total up to 13+10+9+10...=70 ways, for the top rows, so $70^2$ ways
• proceeding this way we get $99^2+70^2+75^2+74^2+55^2+75^2+52^2+59^2+70^2+50^2 +52^2+55^2+41^2=\boxed{55447}$ ways.