Filled With Circles 2
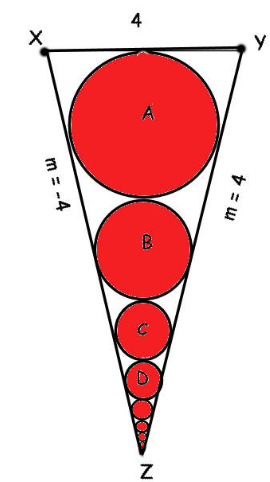
is an isosceles triangle with .
are infinitely many circles tangent to the triangle and to their neighboring circles.
Find the sum of areas of all these circles to 3 decimal places.
The answer is 12.19117.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
∠ C Y O = 2 1 × ( 9 0 ∘ − a r c t a n ( 4 1 ) ) = 3 7 . 9 8 1 8 8 ∘
r = 2 × t a n ( ∠ C Y O ) = 1 . 5 6 1 5 5
b = 8 − 2 r , b a = 8 2 , a = 4 8 − 2 r = 1 . 2 1 9 2 2
Area of trapezoid A B Y X is A t = 2 1 ( 4 + 2 a ) 2 R = 1 0 . 0 5 3 9
Area of the circle centered at O is A c = π r 2 = 7 . 6 6 0 6
The ratio of the areas A t A c = 0 . 7 6 1 9 4 8
This ratio remains the same for all the circles below as well, each within its own trapezoid, so the total area of circles is this ratio times the total area of △ X Y Z
A = 0 . 7 6 1 9 4 8 × 2 1 × 4 × 8 = 1 2 . 1 9 1 1 7