Filling An Ice Cream Cone

Geometry Level 4

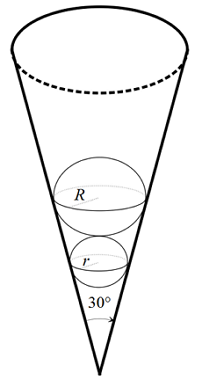
A right circular cone with a vertex angle of $30^{\circ}$ is opened upward. A sphere with a radius $r$ is dropped into the cone. A second sphere, this one with a radius $R$ , is placed on top of it. The second sphere rests in contact with both the bottom sphere as well as the sides of the cone (all the way around). What is the ratio $\dfrac Rr$ ?

Round your answer to 1 decimal place.

The answer is 1.7.

1 solution

Marta Reece
May 20, 2016

Relevant wiki: Similar Triangles - Problem Solving - Medium

Triangles ABC and ADE in the cross-section are similar, therefore the ratio $R/r$ is equal to the ration of AD to AB. The angle BAC is half of the vertex angle, that is $15^{0}$ .

$\frac{R}{r}=\frac{R + r + r\times csc(15^{0})}{r\times csc(15^{0})}$

Multiplying by $r\times csc(15^{0})$ and solving again for the ratio, we'll get

$\frac{R}{r}=\frac{1 + csc(15^{0})}{-1 + csc(15^{0})}=\frac{1+sin(15^{0})}{1-sin(15^{0})}=1.7$

Filling An Ice Cream Cone

The answer is 1.7.

1 solution

0 pending reports