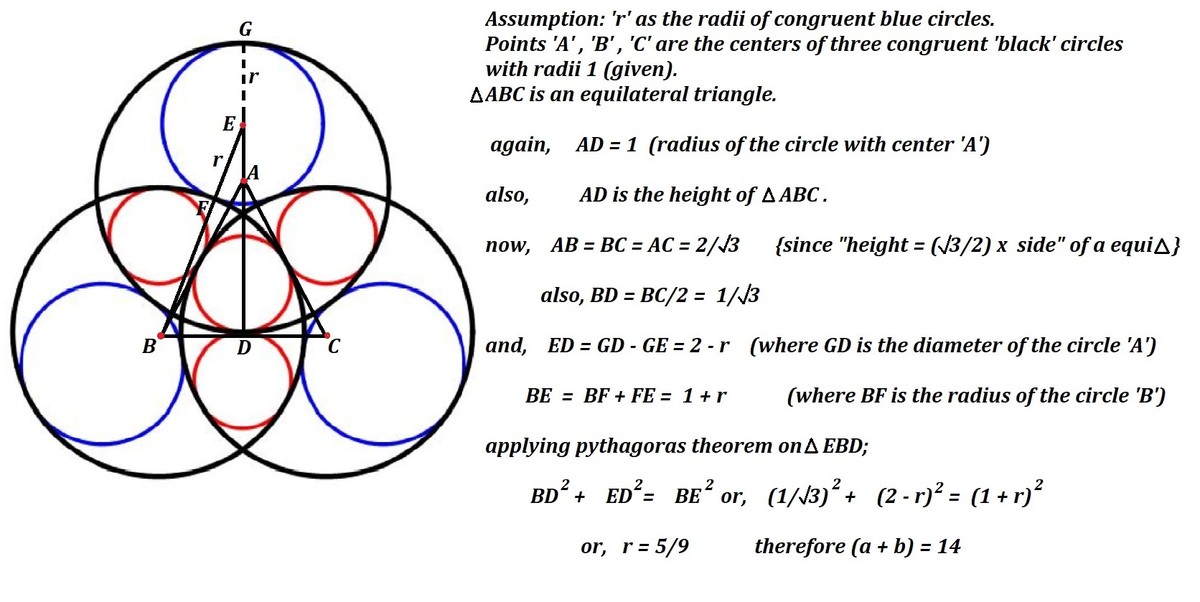
Filling Borromean Rings

Let r be the radius of the red circle. Since all the reds are identical, the points where the middle one is kissing the surrounding ones must be the midpoints of the straight lines connecting the blacks' centers. Now that we've seen that the middle red is fitted snug inside the equilateral triangle formed by blacks' centers, it is obvious that r/(1-r)=1/2, thus r = 1/3 with the triangle's side 2/sqrt(3).
Now let the radius of blue circle be R. Blues are each kissing one black internally and two externally. If we construct a triangle with the centers of a blue and its two external blacks, it will be an isosceles, one that share its base with the original equilateral triangle. Its height will be R less than internal black's diameter and the same sides will be the distance between the blue and external black, that is the sum of their radii = R + 1.
(R + 1)² = (1 / sqrt(3))² + (2 - R)².
2R + 1 = 13/3 - 4R.
R = 5/9
Answer = 5 + 9 = 14

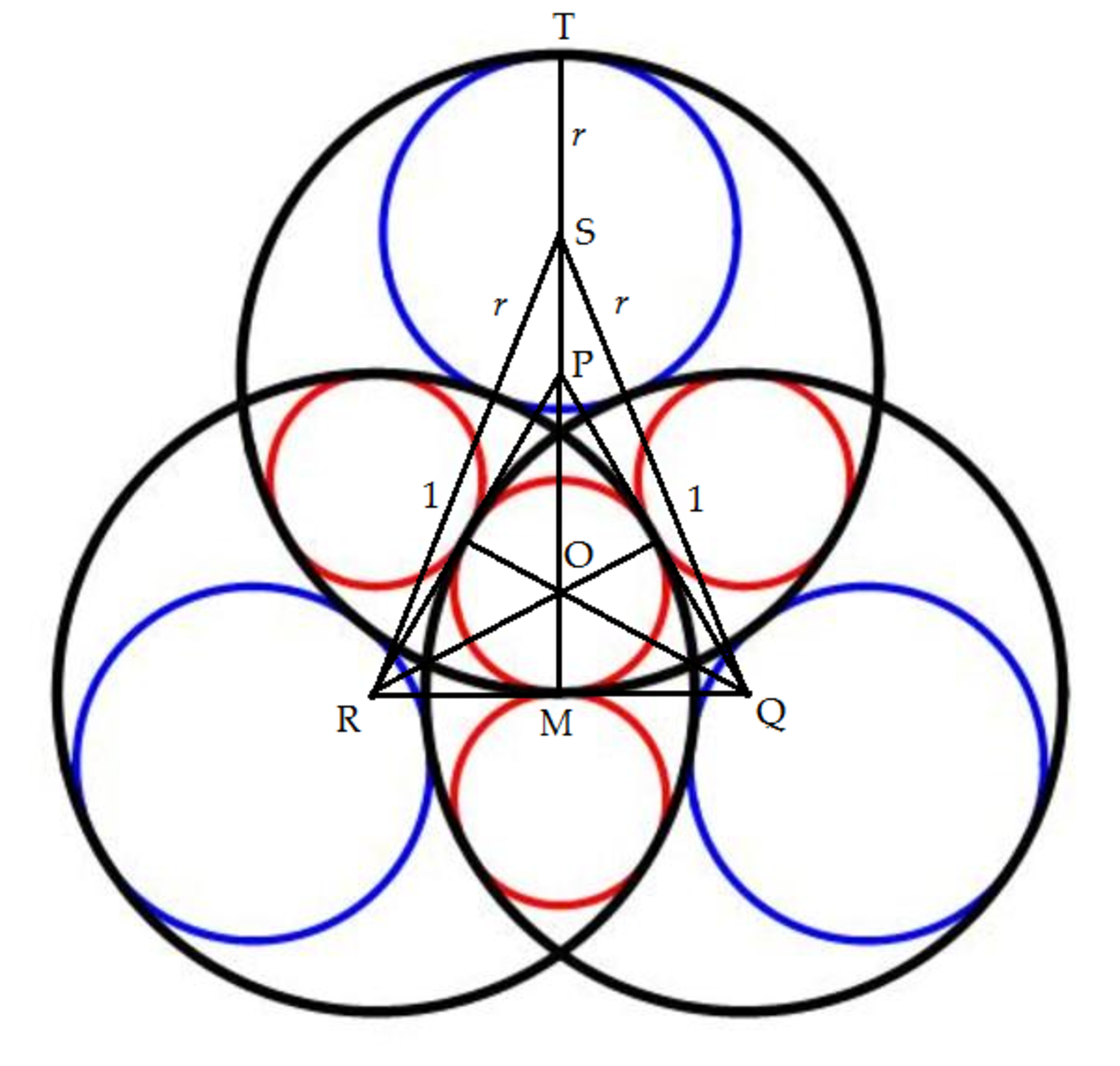
Label the center of the central red circle be $O$ , the centers of the three black circles be $P$ , $Q$ , and $R$ , the center of the top blue circle be $S$ , $M$ is the midpoint of $RQ$ , and the point of the top black and blue circles be $T$ as shown in the figure.

We note that center $O$ is also the centroid of equilateral $\triangle PQR$ and that the median $PM$ is a radius of the black circle hence $PM=1$ . Then $RM=MQ = \frac 1{\sqrt 3}$ and $TM = 2$ . Let the radius of the blue circle be $r$ . By Pythagorean theorem :

$\begin{aligned} RM^2 + SM^2 & = SR^2 \\ \frac 13 + (2-r)^2 & = (1+r)^2 \\ \frac 13 + 4 - 4r + r^2 & = 1 + 2r + r^2 \\ 6r & = \frac {10}3 \\ \implies r & = \frac 59 \end{aligned}$

Therefore $a+b = 5+9 = \boxed{14}$ .

*This answer skips a lot of laborious calculation that I feel adds little insight to the solution

First we note that for all the red circles to be of the same size, the equilateral triangle defined by the centres of the black circles must be tangent to the opposite black circle and two adjacent red circles. Furthermore, it has an altitude of 1 (the radius of the black circle).

From this, it is possible to draw the red and black circles as shown below, where the black circles are defined by ${ x }^{ 2 }+{ \left( y-\frac { 2 }{ 3 } \right) }^{ 2 }=1$ and ${ \left( x\pm \frac { 1 }{ \sqrt { 3 } } \right) }^{ 2 }+{ \left( y+\frac { 1 }{ 3 } \right) }^{ 2 }=1$ while the red circles are defined by $x^{ 2 }+{ y }^{ 2 }={ \left( \frac { 1 }{ 3 } \right) }^{ 2 }$ , $x^{ 2 }+{ \left( y+\frac { 2 }{ 3 } \right) }^{ 2 }={ \left( \frac { 1 }{ 3 } \right) }^{ 2 }$ and ${ \left( x\pm \frac { 1 }{ \sqrt { 3 } } \right) }^{ 2 }+{ \left( y-\frac { 1 }{ 3 } \right) }^{ 2 }={ \left( \frac { 1 }{ 3 } \right) }^{ 2 }$ .

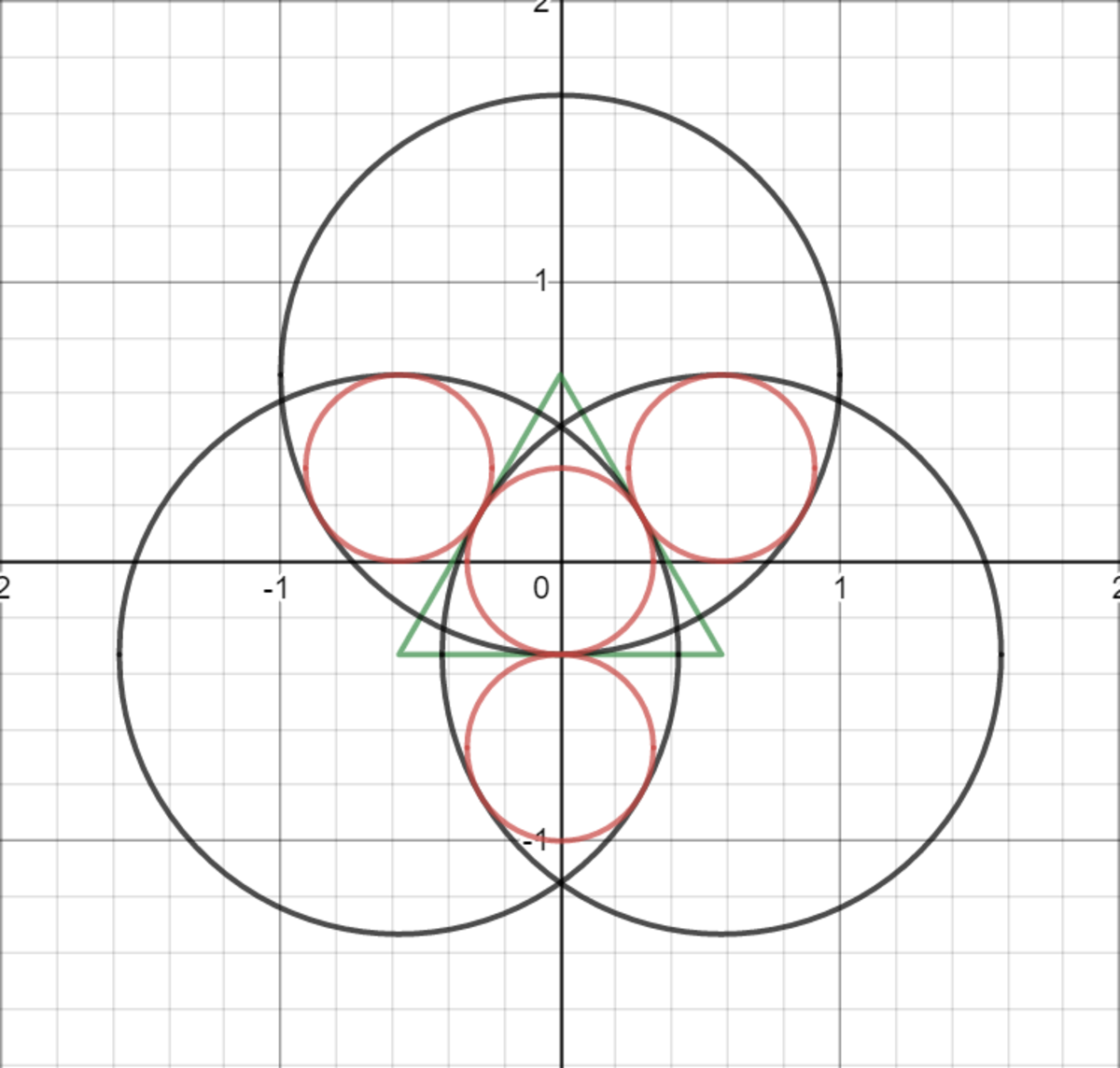
From here, we invert the entire diagram with respect to the center red circle, where circle inversion is given by the mapping of a point $P$ to its inverse $P'$ with respect to a reference circle of radius $r$ and center $O$ with the equation $\left| OP \right| \left| OP' \right| ={ r }^{ 2 }$ . A key property of circle inversion to take note of is that tangent points and intersections are preserved after inversion.

The black circles are inverted onto the purple circles on the opposite side, i.e. ${ x }^{ 2 }+{ \left( y-\frac { 2 }{ 3 } \right) }^{ 2 }=1$ inverts to ${ x }^{ 2 }+{ \left( y+\frac { 2 }{ 15 } \right) }^{ 2 }={ \left( \frac { 1 }{ 5 } \right) }^{ 2 }$ and ${ \left( x\pm \frac { 1 }{ \sqrt { 3 } } \right) }^{ 2 }+{ \left( y+\frac { 1 }{ 3 } \right) }^{ 2 }=1$ to ${ \left( x\mp \frac { \sqrt { 3 } }{ 15 } \right) }^{ 2 }+{ \left( y-\frac { 1 }{ 15 } \right) }^{ 2 }={ \left( \frac { 1 }{ 15 } \right) }^{ 2 }$ . The blue circle represents the image of the original blue circle after inversion. Notice how it remains tangent to the purple circles but not the red reference circle. Take note that the inner green triangle is NOT the inversion of the outer green triangle.

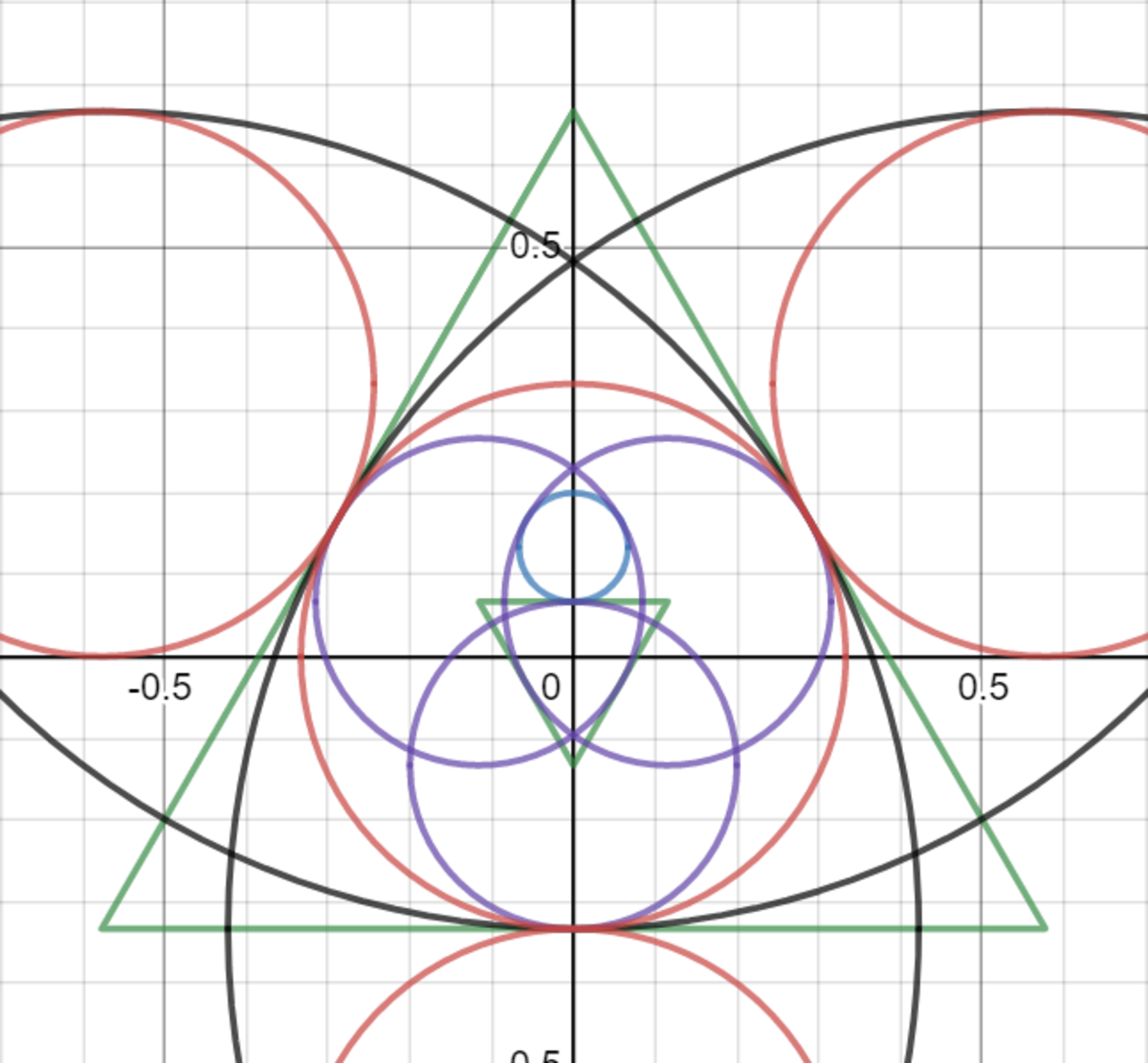
This blue circle has a center that is a mirror reflection of the opposite purple circle, at $\left( 0,\frac { 2 }{ 15 } \right)$ . This will be explained in a comment below. By noting that the inner green triangle is completely analogous to the outer green triangle, we can reason that the center of the blue circle must a distance two times its radius from the origin (note that the center of a red circle is two radii away from the origin in the original diagram). Hence, the blue circle has a radius $\frac { 1 }{ 2 } \times \frac { 2 }{ 15 } =\frac { 1 }{ 15 }$ . Finally, by inverting the closest and furthest points of the blue circle back to the original domain, we can calculate that its radius is $\boxed{\frac { 5 }{ 9 } }$ .

---

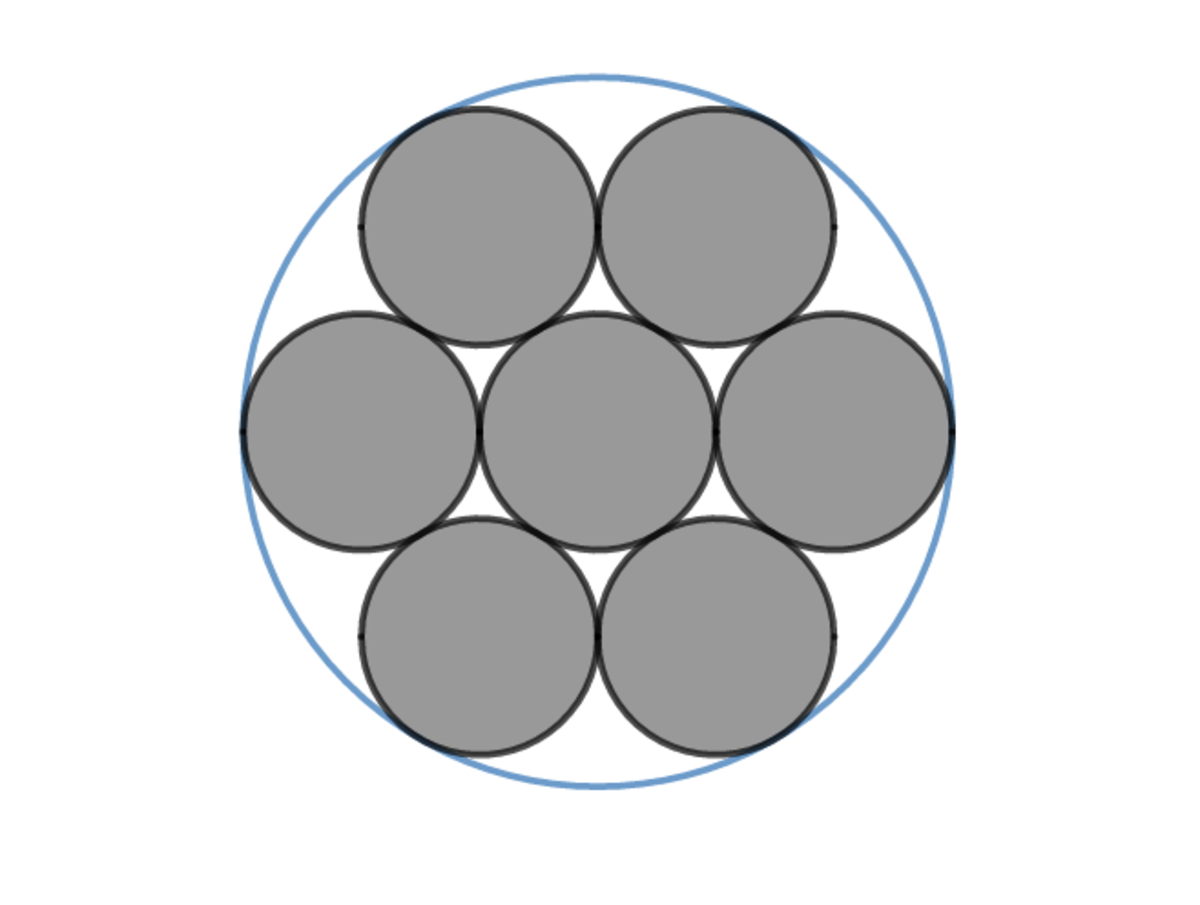
The reason why the blue circle has a center that is a reflection symmetry of the purple circle about the origin is due to the optimal circle packing of 7 identical unit circles within a larger circle. The optimal solution is to arrange the 7 unit circles into a hexagon shape with one circle in the center, as shown.

Due to the repeating nature of hexagons, we can extend the hexagon shape to beyond the original enclosing circle, C_1, to form another hexagon centered on one of the edge circles inside ${ C }_{ 1 }$ . In order for the center and two adjacent circles such as the red circles in the question to all be tangent to the same larger circle, ${ C }_{ 2}$ , this circle must be centered on the edge unit circle between the red circles. Since this edge unit circle is a mirror reflection symmetry of the opposite unit circle, the center of ${ C }_{ 2}$ must also be a reflection of the center of the opposite unit circle.

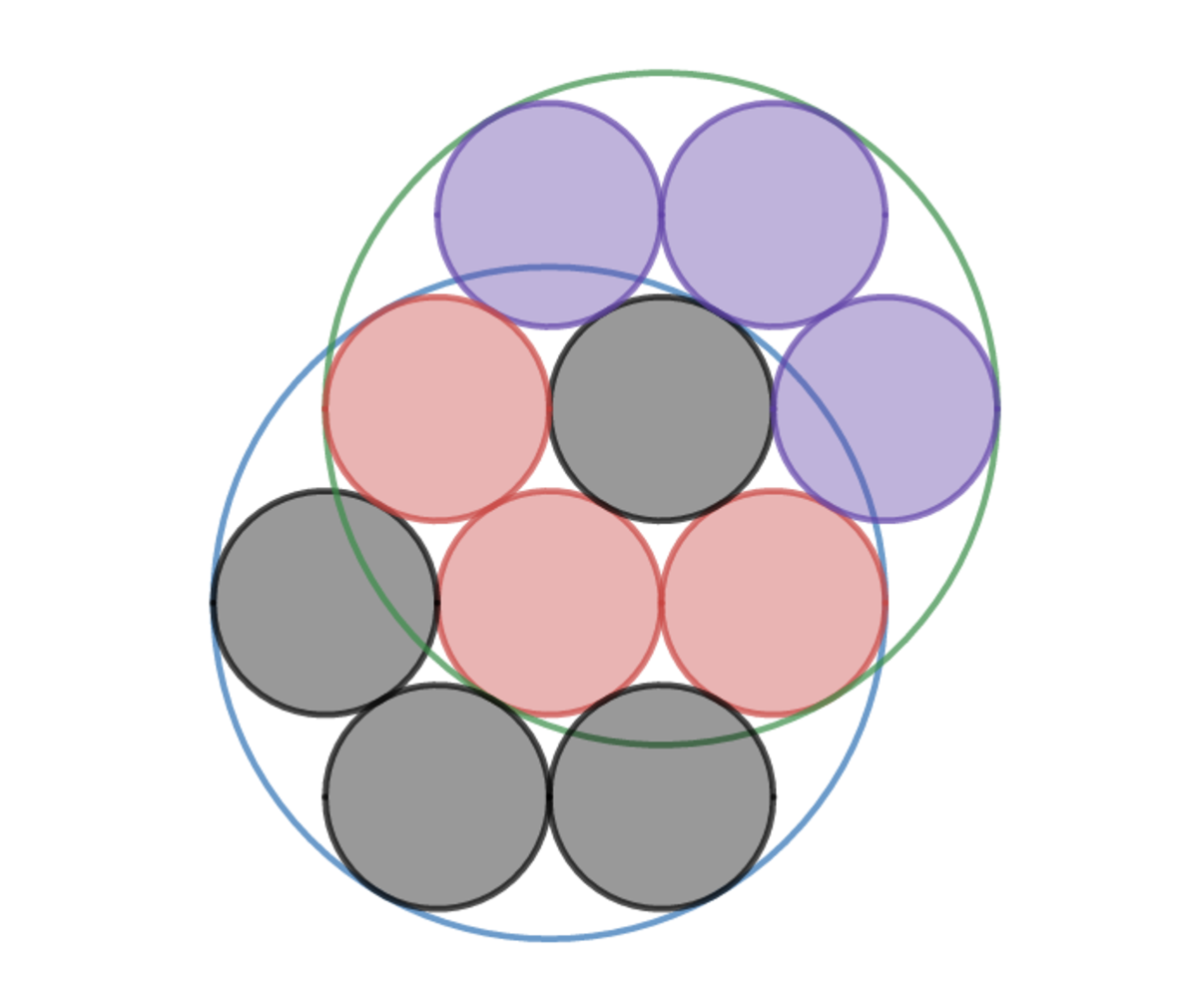
In this diagram, the green circle represents ${ C }_{ 2}$ and is directly analogous to the black circles and their inversion the purple circles. Hence their centers are a reflection of, respectively, the opposite red circle and the opposite blue circle.