Fillomino solutions redux
 Consider a
polyomino
. We want to divide
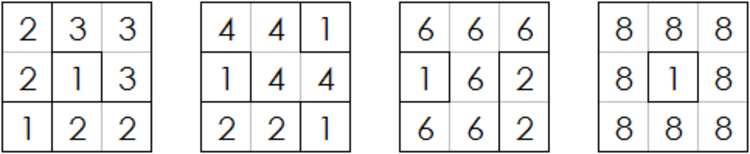
into several (may be one) smaller polyominoes. The division is called a
Fillomino
solution
if no two polyominoes of equal size share a side. (They may touch at a point.) In other words, the division is a valid solution of a Fillomino puzzle.
Consider a
polyomino
. We want to divide
into several (may be one) smaller polyominoes. The division is called a
Fillomino
solution
if no two polyominoes of equal size share a side. (They may touch at a point.) In other words, the division is a valid solution of a Fillomino puzzle.
Determine the number of distinct Fillomino solutions of the square.
Try here for an easier version, or here for a much harder version.
The answer is 445.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Depth-first Search
This is a more difficult version of the previous problem; instead of 2 × 3 , we have 3 × 3 . The solution is thus to use programming, a simple exercise in brute force:
Here,
size(G, x, y)takes a two-dimensional list (supposedly the grid) and returns the "size" of the polyomino containing the square ( x , y ) . (Here x is the row number and y is the column-number, both zero-indexed. The polyomino is the largest region containing all the same element.) This is just a simple depth-first-search -based flood fill , keeping track of the size.check(G)is the checking algorithm, testing whether the gridGis a valid Fillomino solution. The idea is simply to check whether the size of each square is equal to the number written in the square.solve(candidates, r, c)is a simple function to compute the number of solutions for a given candidate list for an r × c rectangle. The idea is just to brute force: each cell is attempted with each possible number, and the result is checked withcheck.At this point, it's actually possible to solve simply with
solve([1,2,3,4,5,6,7,8,9], 3, 3); however, it takes a long time, so some speedup is required. My speedup is to notice that:solve([1,2,3,6], 3, 3) - solve([1,2,3], 3, 3).On my machine, this runs for approximately 20 seconds. Still long, but at least far better than attempting the naive
solve([1,2,3,4,5,6,7,8,9], 3, 3).The result is 4 4 5 .