Fillomino solutions

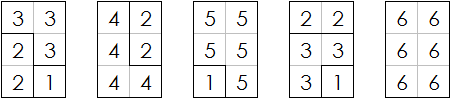
This is a simple problem that can be done by hand:

• There is $1$ containing a 6-mino: the whole rectangle is not divided at all.
• There are $6$ containing a 5-mino: remove any one square and the rest makes a 5-mino. The removed square must be a 1-mino.
• There are $10$ containing a 4-mino. There are two removed squares (leaving the rest a 4-mino); however, these removed squares cannot separate a corner off (the rest is a 1-mino and a 3-mino, not a 4-mino), and they cannot be both from the middle row (the rest is two 2-minoes). This removes $5$ out of $\binom{6}{2} = 15$ possibilities, for a total of $10$ .

There are $16$ more, where all minoes have size not greater than 3.

Note that it's impossible to not have any 3-mino. (Suppose it's possible. If a corner square is 1, it forces the two squares adjacent to it to be 2. One of them is also a corner square, and it's forced to go to the middle row; this makes the two 2-minoes to merge.

Thus, all corner squares must be 2. This leaves no place for the middle row.

Also note that we cannot have two 3-minoes, since they collectively complete 6 cells and thus the entire rectangle. So we have one 3-mino.

• This 3-mino can be "around" the rectangle; not both middle row cells are occupied. The remaining space is also a 3-mino, that can be filled in two ways (one 1-mino on one end, and the rest is a 2-mino). There are $6$ ways to put the 3-mino, times $2$ to fill the rest, for a total of $12$ ways.
• This 3-mino can also "cut" the rectangle, occupying both middle row cells. This separates the rest into a 1-mino and a 2-mino. There are $4$ such ways.

In total, there are $1+6+10+16 = \boxed{33}$ ways to fill this.

Of course, the intended answer is to use programming, and you're unlikely to be able to solve the harder version without it...