Filtered Curve vs. Original (Part 2)
Two discrete curves are defined as follows:
Δ x = 1 0 0 0 π α = 0 . 9 9 5 k = 0 , 1 , 2 , 3 . . . . 2 0 0 0 x k = k Δ x y k = s i n ( x k ) y k ′ = α y k − 1 ′ + ( 1 − α ) y k y 0 ′ = 0
Both curves are plotted on the diagram as smooth lines for display purposes. The k subscript denotes the present value of the variable, and the k − 1 subscript denotes the previous value of the variable. The quantity y ′ is the result when y is passed through an infinite-impulse-response filter.
Define the infinitesimal area and total area between curves as follows:
Δ A k = ∣ y k − y k ′ ∣ Δ x A = Σ k = 0 k = 2 0 0 0 Δ A k
What is the value of A ?
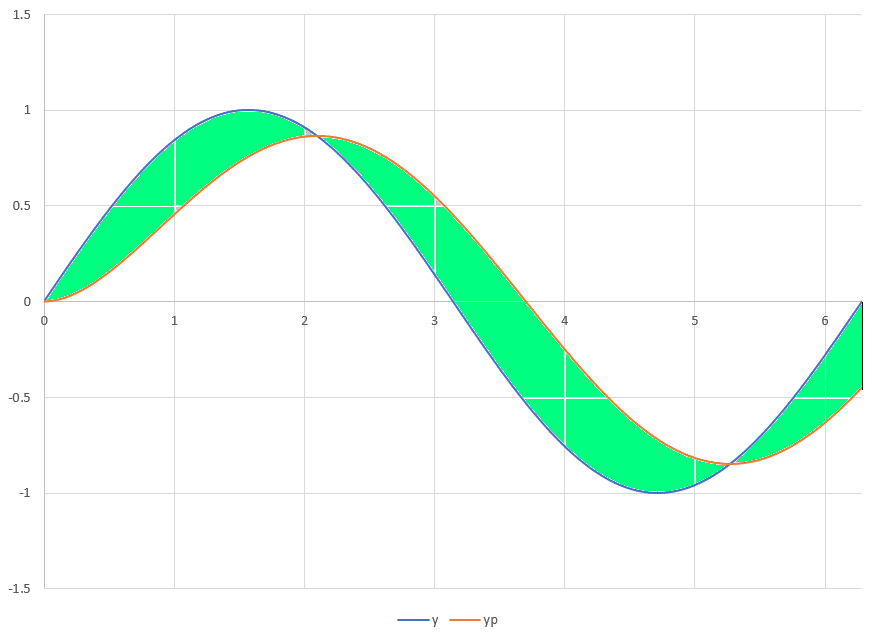
The answer is 1.8574.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!