The Ins And Outs Of Circles
⎩ ⎪ ⎨ ⎪ ⎧ x 2 + y 2 ( x − 1 ) 2 + ( y − 1 ) 2 ( x + 1 ) 2 + ( y + 1 ) 2 ≤ 1 ≥ 1 ≥ 1
Let D be the domain of the system of inequalities shown above. What is the area of D ?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Ah. You beat me to it - and with a lovely diagram.. What did you use to create such a neat-looking image?
Log in to reply
It's called GeoGebra (link: https://www.geogebra.org/). It's an amazing software that provides tools for analysis, geometry, algebra and even 3D graphing!
Log in to reply
Nice graph by the way. I thought of creating the solution, but you beat me too! XD
GeoGebra is the good way to graph the equation. Desmos is another website where you can create graphs too!
Very clear solution!
A nice way to present a familiar problem. (-: The region is outlined by 4 quarter circle arcs of unit radius with those in the 1st and 3rd quadrant concave and those in the 2nd and 4th quadrant convex. This means if we split the region into 4 parts corresponding to each quadrant we can rearrange them to make two unit squares. A diagram would probably be clearer... Anyone?
If we sketch down the three inequalities, we notice that they are circles, overlapping in this way: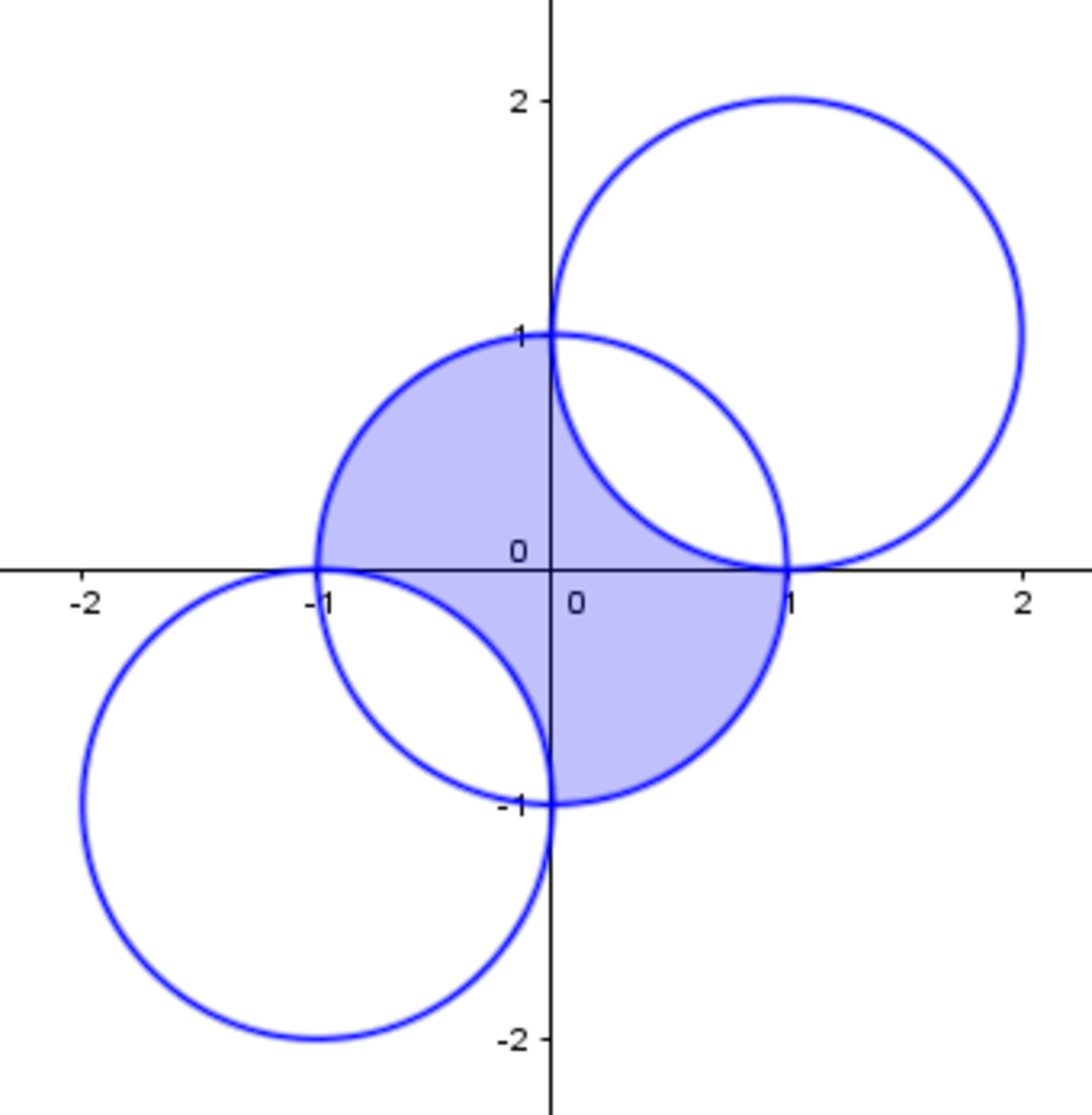
The blue part represents the domain of our system, since we have to find all the points that are both internal to the circle corresponding to the first expression, and external to the other two. Now, we might notice that this area can be reduced to a square of side 2 (imagine cutting along the segments that go respectively from the point ( 1 , 0 ) to the point ( 0 , − 1 ) , and from the point ( 0 , 1 ) to the point ( − 1 , 0 ) and attaching the resulting pieces forming the square), thus the area is 2