Fit just nicely

Base from my figure above, we can use the derived formula

$\boxed{x=\dfrac{bh}{b+h}}$ note: I did not include the derivation.

$b=\sqrt{6^2+6^2}=\sqrt{72}=6\sqrt{2}$

$h=\sqrt{6^2-\left(\dfrac{6\sqrt{2}}{2}\right)^2}=\sqrt{18}=3\sqrt{2}$

Substitute the values on the formula.

$x=\dfrac{(6\sqrt{2})(3\sqrt{2})}{6\sqrt{2}+3\sqrt{2}}=\dfrac{18(2)}{9\sqrt{2}}=\dfrac{36}{9\sqrt{2}}=4\sqrt{2}$

Solving for the area, we have

$x^2=\left(\dfrac{4}{\sqrt{2}}\right)^2=$ $\boxed{8}$

its very easy , let SPDF have a side - x , in triangle FPC base angles each 45 because the big triangle is isosceles right angled triangle. so ,PC = FP = x similarly SD = BD = X and already PD = x BC = BD + PD + PC = 3X and by pythagorous theorem BC = $6\sqrt { 2 }$ , x = $2\sqrt { 2 }$ area = ${ x }^{ 2 }$ = 8

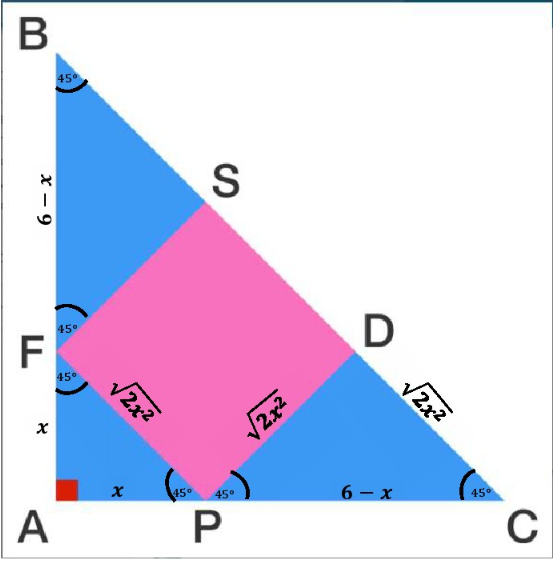
Since $ABC$ is an isosceles right triangle, $\angle{B}=\angle{C}=45^{\circ}$ . Of course, $\triangle{BSF},~\triangle{FAP}, \text{and}~\triangle{PDC}$ are isosceles right triangles too. Let $AF=AP=x$ , by pythagorous theorem we have $FP=\sqrt{2x^2}$ and since $SDPF$ is a square then $SF=SD=DP=\sqrt{2x^2}$ . Now, look at the $\triangle{PDC}$

$\begin{aligned}\left(6-x\right)^2&=2x^2+2x^2\\6-x&=2x\\x&=2\end{aligned}$

Thus, the area of the square $SDPF=2x^2=8$ . $_\square$

Let $x = (SA)$ . Then $(SD) = (SF) = \sqrt{2} * x$ , and so $(SB) = 2x$ .

Thus $(AB) = (SA) + (SB) = x + 2x = 3x = 6 \Longrightarrow x = 2$ .

The square $SPDF$ thus has sides lengths $\sqrt{2} * x = 2\sqrt{2}$ cm., and hence has an area of $\boxed{8} cm^{2}$ .

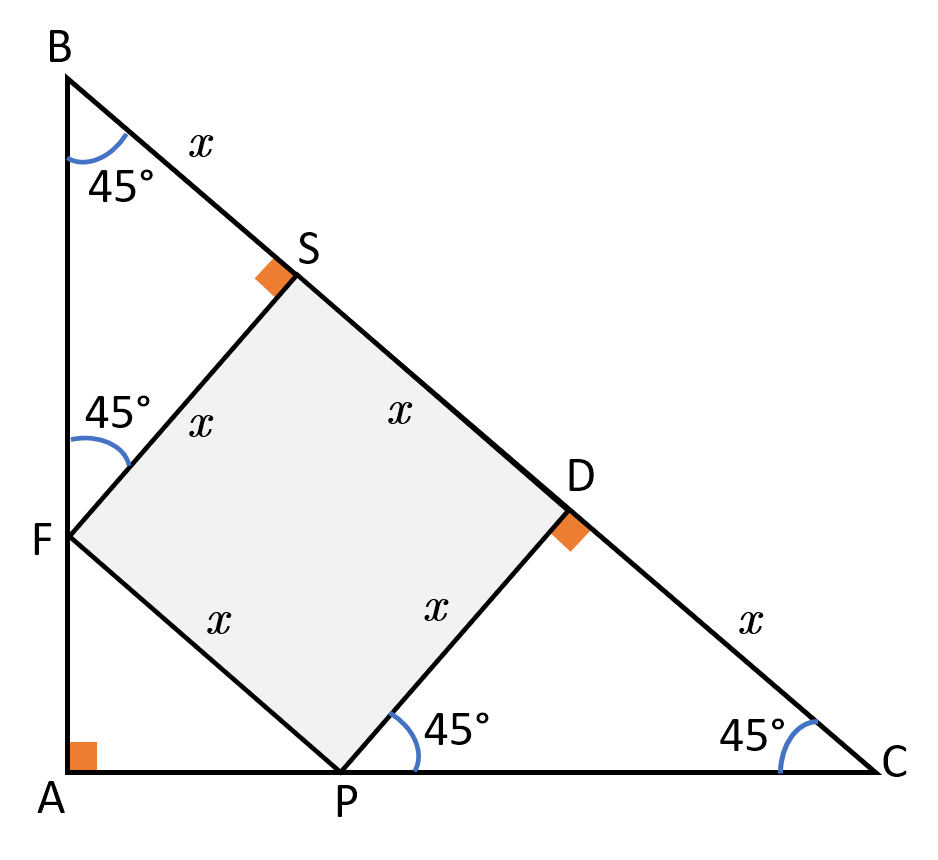
Let the side of the square be $x$

Since $ABC$ is an isosceles right angled triangle, $\angle ABC = \angle ACB = 45 ^ \circ$

$\angle BFS = \angle DPC = 180^\circ-(90^\circ+45^\circ) = 45^\circ$

Therefore, both $BSF$ and $PDC$ are isosceles triangles and $BS = DC = x$ .

Hence, $BC= BS+SD+DC = 3x$

Using Pythagoras theorem in triangle $ABC$ ,

$AB^2 + AC^2 = BC^2$

$6^2+6^2 = (3x)^2$

$72 = 9x^2$

$x^2 =$ Area of the square $SDPF = \boxed{8}$ square units.

Triangle BSF and Triangle PDC are both 45- 45-90 triangle, meaning it's isosceles. BS=SF & PD = DC Let them be x, so the area of the square is x^2 BS+SD+DC=3x sqrt(2*6^2)=3x x= 2 sqrt (2) x^2=8 8 is the answer.

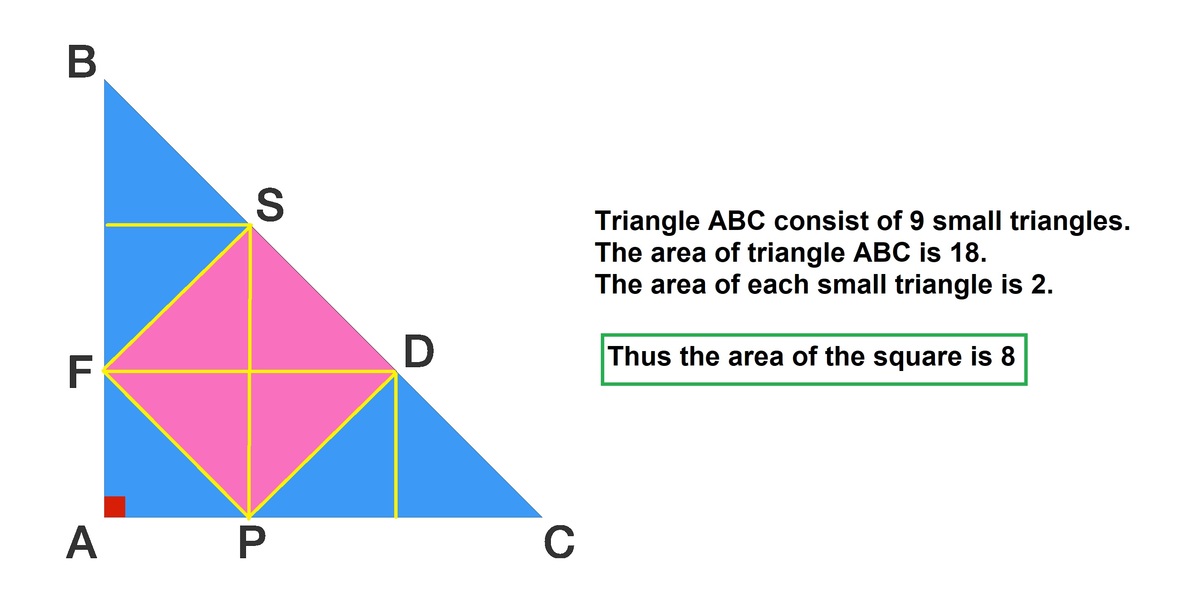
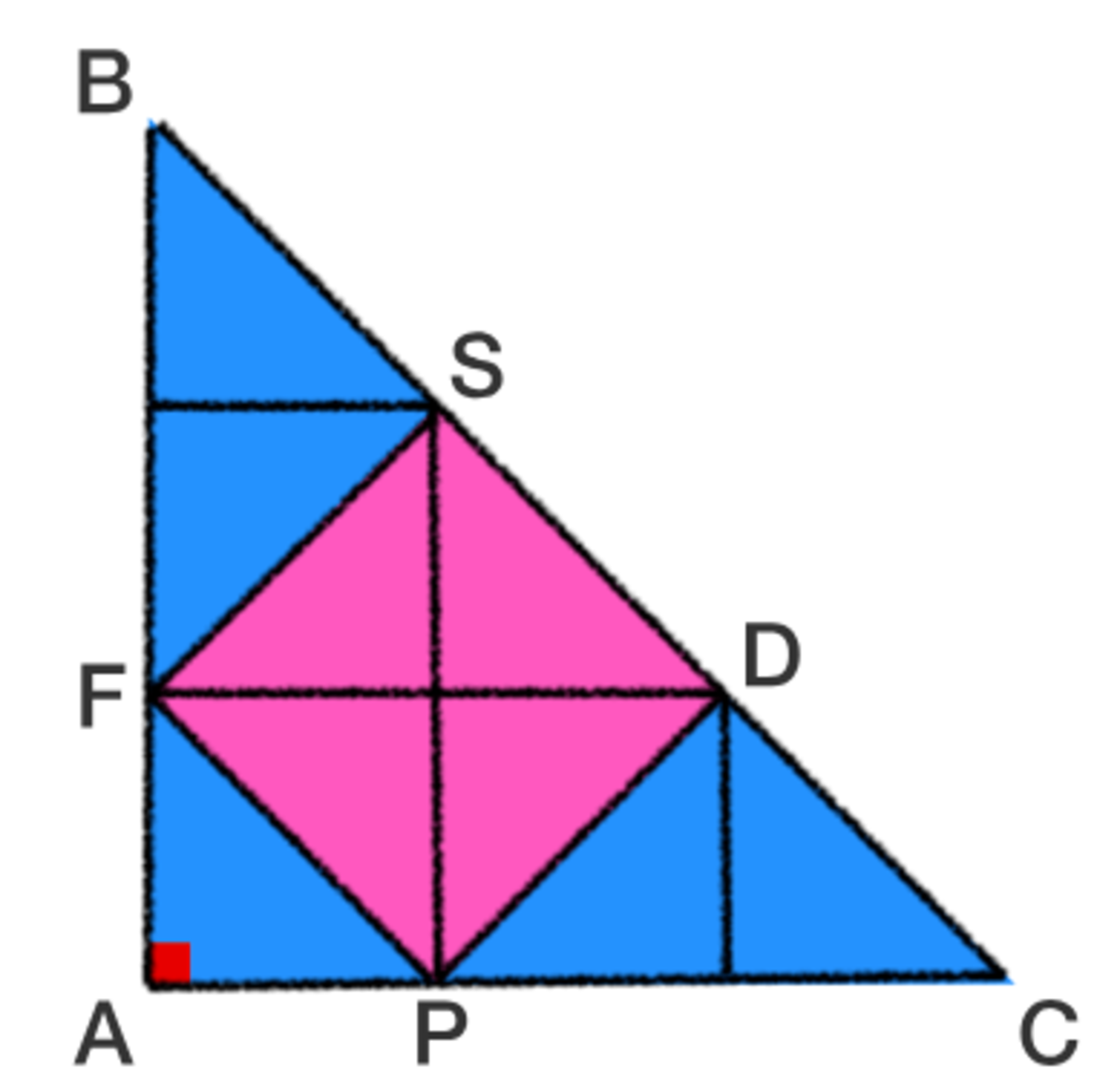as you see this shape is made of 9 identical triangles. and the square is made of 4 of the triangles. the area of the triangle is 6*6/2=18. since the square takes up 4/9 of the triangle, 4/9 * 18 = 8

Triangle ABC has area 18 and can be split into nine congruent triangles (all of which are congruent to triangle AFP) each with area 2. Square FSPD is comprised of four of these triangles and therefore has area 8.

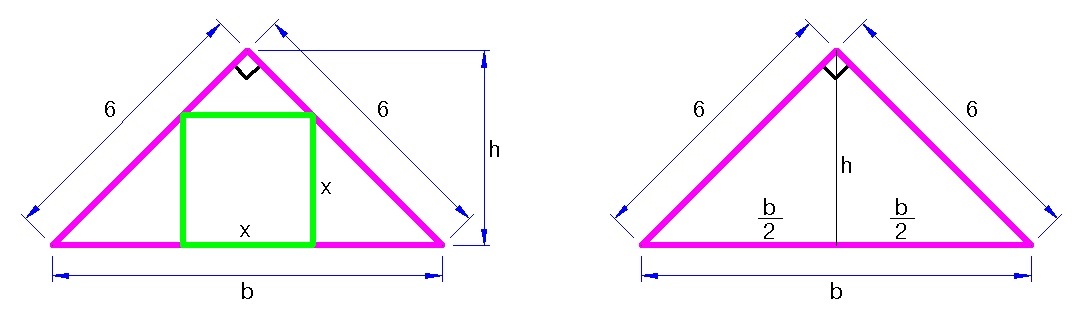Based from my figure, let $h$ be the height and $b$ be the base of the triangle

Solving for the base, we have

$b=\sqrt{6^2+6^2}=6\sqrt{2}$

Solving for the height, we have

$h=\sqrt{6^2-(\frac{6}{2}\sqrt{2})^2}=3\sqrt{2}$

Now use the formula $x=\dfrac{bh}{b+h}$ (this is in reference with the figure on the left), we have

$x=\dfrac{bh}{b+h}=\dfrac{(6\sqrt{2})(3\sqrt{2})}{6\sqrt{2}+3\sqrt{2}}=\dfrac{4}{\sqrt{2}}$

Finally, the area of the square is

$x^2=(\dfrac{4}{\sqrt{2}})^2=$ $\large\color{#D61F06}\boxed{8}$