Replicate to Solve
Let ABC be an isosceles triangle in which Angle BAC = 20 degrees and AB=AC. Let D be a point on the side AC such that AD=BC. Find Angle ABD.
(This is from a source of problems for practice, but without hints or solutions, so they're challenges For anyone who wants to checks it out, the source is this: Challenges And Thrills In Pre-College Mathematics)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
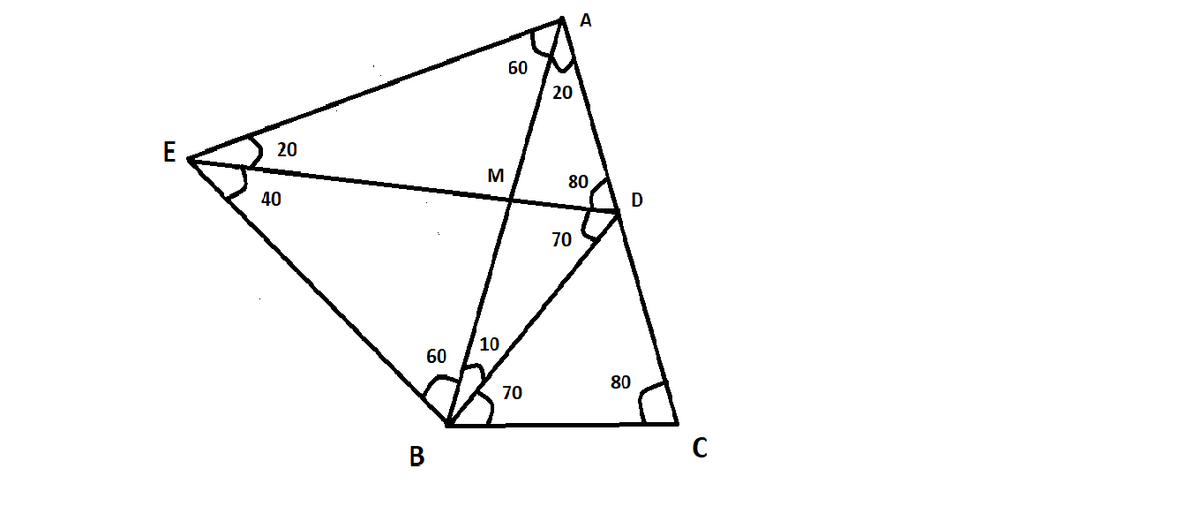
Let ∠ A B D = α . Then
sin 2 0 ° ∣ B D ∣ = sin α ∣ A D ∣
sin 8 0 ° ∣ B D ∣ = sin ( 2 0 ° + α ) ∣ B C ∣ = sin ( 2 0 ° + α ) ∣ A D ∣
⟹ sin 8 0 ° sin α = sin 2 0 ° sin ( 2 0 ° + α )
⟹ tan α = sin 8 0 ° − sin 2 0 ° cos 2 0 ° sin 2 2 0 ° = tan 1 0 °
⟹ α = 1 0 ° .