Find ∠ B A C
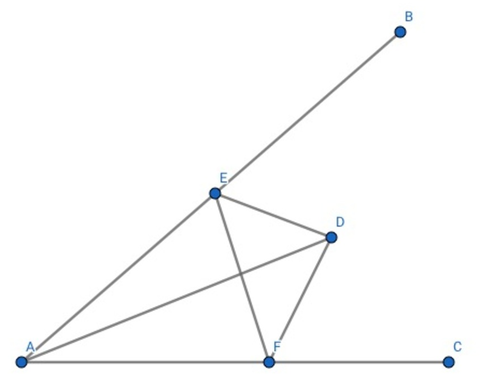
As shown in the figure above, point D is any point within ∠ B A C and A D = 5 , while E and F are the moving points on A B and A C respectively. If the shortest perimeter of △ D E F is 5 , find the measure of ∠ B A C in degree.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
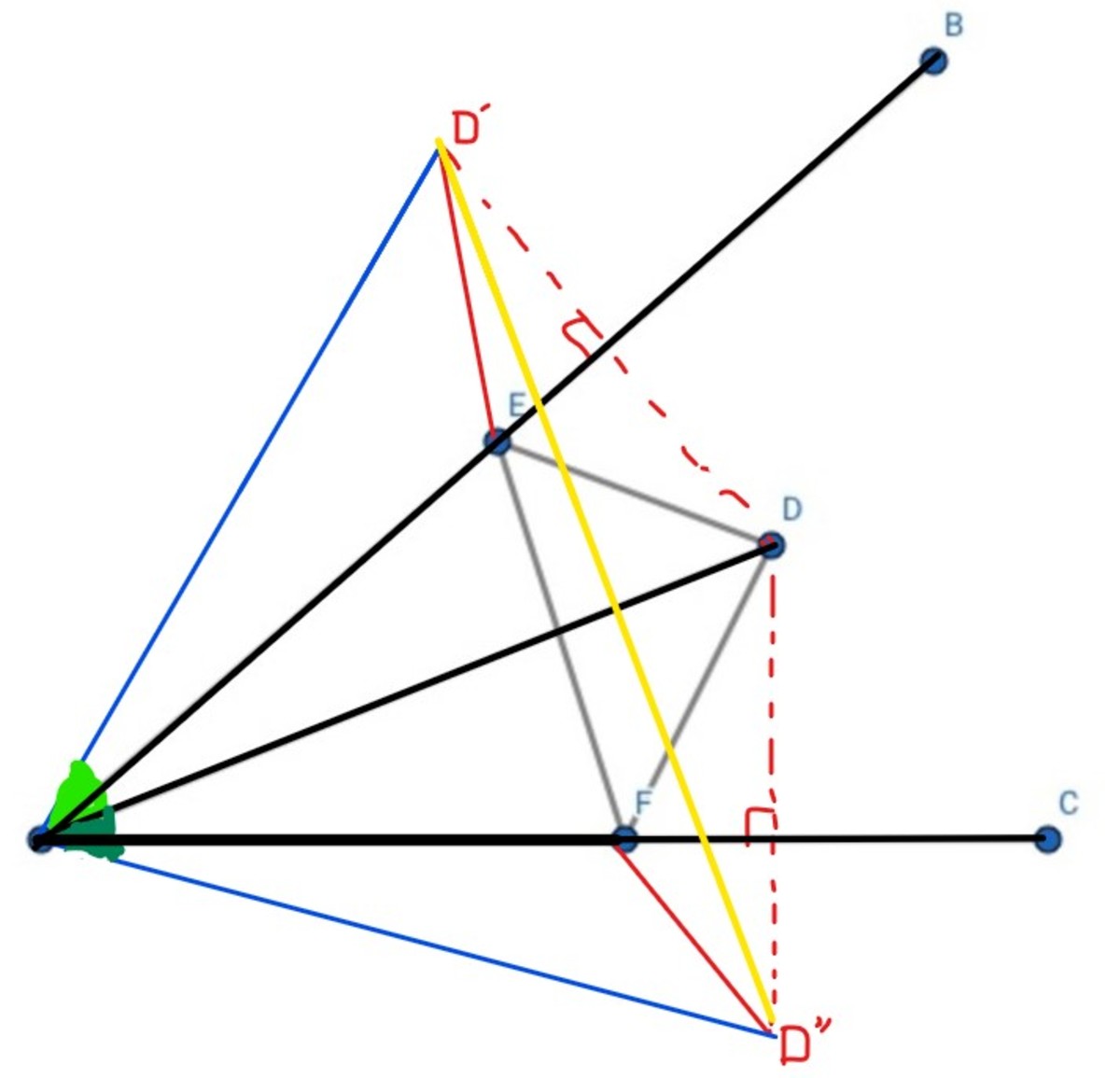 The photo of explanation
Let
D
′
and
D
′
′
be the reflection of
D
about
A
B
and
A
C
respectively. Then,
min
(
C
△
D
E
F
)
=
min
(
D
E
+
E
F
+
F
D
)
=
min
(
D
′
E
+
E
F
+
F
D
′
′
)
=
D
′
D
′
′
=
5
. Observe that
△
A
D
′
D
′
′
is a equilateral triangle, therefore
∠
D
′
A
D
"
=
6
0
°
. Also, by the reflection,
∠
B
A
D
=
∠
B
A
D
′
and
∠
C
A
D
=
∠
C
A
D
′
′
. Therefore,
∠
D
′
A
D
"
=
∠
B
A
D
+
∠
B
A
D
′
+
∠
C
A
D
+
∠
C
A
D
′
′
=
2
(
∠
B
A
D
+
∠
C
A
D
)
=
2
∠
B
A
C
=
2
α
°
=
6
0
°
→
α
=
3
0
The photo of explanation
Let
D
′
and
D
′
′
be the reflection of
D
about
A
B
and
A
C
respectively. Then,
min
(
C
△
D
E
F
)
=
min
(
D
E
+
E
F
+
F
D
)
=
min
(
D
′
E
+
E
F
+
F
D
′
′
)
=
D
′
D
′
′
=
5
. Observe that
△
A
D
′
D
′
′
is a equilateral triangle, therefore
∠
D
′
A
D
"
=
6
0
°
. Also, by the reflection,
∠
B
A
D
=
∠
B
A
D
′
and
∠
C
A
D
=
∠
C
A
D
′
′
. Therefore,
∠
D
′
A
D
"
=
∠
B
A
D
+
∠
B
A
D
′
+
∠
C
A
D
+
∠
C
A
D
′
′
=
2
(
∠
B
A
D
+
∠
C
A
D
)
=
2
∠
B
A
C
=
2
α
°
=
6
0
°
→
α
=
3
0
Consider △ A B C with side lengths a , b , and c . With a common base b , using AM-GM inequality , we have a + c ≥ 2 a c . That is the shortest a + c occurs when a = c or for a common base, an isosceles triangle has the shortest perimeter. Therefore for a common base E F , the shortest perimeter occurs when △ D E F is isosceles or A D bisects ∠ B A C and E F ⊥ A D . Let E F cuts A D at P , A P = x , and E P = y . Then the perimeter of △ D E F is given by p = 2 y + 2 y 2 + ( 5 − x ) 2 . Let ∠ B A C = θ and t = tan 2 θ ; then y = x tan 2 θ = t x and:
2 p 2 1 ⋅ d x d p = t x + t 2 x 2 + ( 5 − x ) 2 = t + t 2 x 2 + ( 5 − x ) 2 t 2 x + x − 5
Extrema occur when d x d p = 0 , we have:
t t 2 x 2 + ( 5 − x ) 2 t 2 ( 1 + t 2 ) x 2 − 1 0 t 2 x + 2 5 t 2 ( 1 + t 2 ) x 2 − 1 0 x + 2 5 ( 1 − t 2 ) ( x − 5 ) 2 + t 2 ( x 2 − 2 5 ) ( x − 5 ) ( x − 5 + t 2 ( x + 5 ) ) = − ( t 2 x + x − 5 ) = ( 1 + 2 t 2 + t 4 ) x 2 − 1 0 ( 1 + t 2 ) x + 2 5 = 0 = 0 = 0 Squaring both sides
⟹ ⎩ ⎨ ⎧ x = 5 x = 1 + t 2 5 ( 1 − t 2 ) ⟹ p = 2 0 t ⟹ p = 1 + t 2 2 0 t when p is maximum. when p is minimum.
Therefore, 1 + t 2 2 0 t = 1 0 sin θ = 5 ⟹ sin θ = 2 1 ⟹ θ = 3 0 ∘ .
8 S S/abc=5(perimeter of triangle orthique) ;S=absinC/2=5*c/2;donc:sinC=1/2-----C=30