Find Area From Versines
Triangle A B C is inscribed in a circle. Versines (green) are drawn from the midpoints of the sides of the triangle perpendicular to them. They have lengths as shown in this figure.
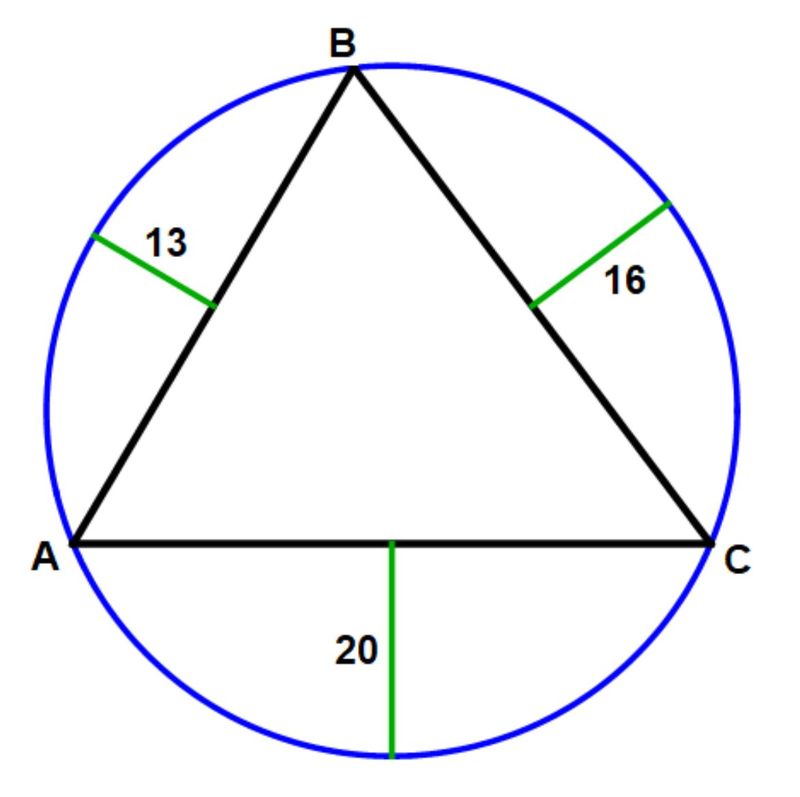
Find the area of △ A B C .
The answer is 1344.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
It's interesting to see how quickly you've arrived at the relation v A v B v C = 2 1 R r 2 ., which had been the inspiration for this problem.
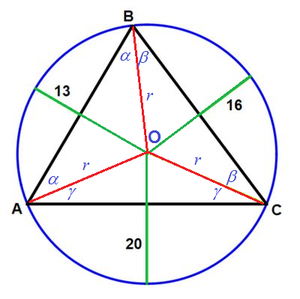
Extending the three versines will meet at the circumcenter O of △ A B C and △ A B C will be split into three isosceles triangles. Let the circumradius be r and the angles of the isosceles triangles be α , β , and γ as shown in the figure. Then sin α = r r − 1 3 , sin β = r r − 1 6 , and sin γ = r r − 2 0 and
2 ( α + β + γ ) α + β + γ α + β cos ( α + β ) cos α cos β − sin α sin β cos α cos β r 2 a r − a 2 ⋅ r 2 b r − b 2 a b ( 2 r − a ) ( 2 r − b ) = 1 8 0 ∘ = 9 0 ∘ = 9 0 ∘ − γ = cos ( 9 0 ∘ − γ ) = sin γ = sin γ = sin α sin β + sin γ = r r − a ⋅ r r − b + r r − c = 2 r 2 − ( a + b + c ) r + a b where a = 1 3 , b = 1 6 , c = 2 0 Squaring both sides
4 a b r 2 − 2 a b ( a + b ) r + a 2 b 2 = 4 r 4 − 4 ( a + b + c ) r 3 + ( ( a + b + c ) 2 + 4 a b ) r 2 − 2 a b ( a + b + c ) r + a 2 b 2
⟹ 4 r 3 − 4 ( a + b + c ) r 2 + ( a + b + c ) 2 r − 2 a b c 4 r 3 − 1 9 6 r 2 + 2 4 0 1 r − 8 3 2 0 ( 2 r − 6 5 ) ( 2 r 2 − 3 3 r + 1 2 8 ) = 0 = 0 = 0
⟹ r = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 2 6 5 = 3 2 . 5 4 3 3 + 6 5 ≈ 1 0 . 2 6 6 4 3 3 − 6 5 ≈ 6 . 2 3 4 ⟹ the acceptable r = 3 2 . 5 and the area of △ A B C is
A △ = r 2 ( sin α cos α + sin β cos β + sin γ cos γ ) = r 2 ( r 2 ( r − 1 3 ) 1 3 ( 2 r − 1 3 ) + r 2 ( r − 1 6 ) 1 6 ( 2 r − 1 6 ) + r 2 ( r − 2 0 ) 2 0 ( 2 r − 2 0 ) ) = ( r − 1 3 ) 1 3 ( 2 r − 1 3 ) + ( r − 1 6 ) 1 6 ( 2 r − 1 6 ) + ( r − 2 0 ) 2 0 ( 2 r − 2 0 ) = 1 9 . 5 ⋅ 2 6 + 1 6 . 5 ⋅ 2 8 + 1 2 . 5 ⋅ 3 0 = 1 3 4 4
The relation 4 r 3 − 4 ( a + b + c ) r 2 + ( a + b + c ) 2 r − 2 a b c = 0 is the same as in Mark Hennings' solution, but arrived at by different means. Fun to see both approaches.
Log in to reply
A beautiful problem, thank you for sharing it with us. Finding the cubic equation for r appears to be the essential intermediate step. By the clever choice of a, b and c, it turns out to have a simple, rational solution. Computing the triangle area then becomes relatively straightforward.
->From the cosine law we know that : c²=a²+b²-2ab.cos(C)
->From the product of chords in a circle we know that in this case
a²=64(2r-16)
b²=80(2r-20)
c²=52(2r-13)
->We also know that the radius r can be expressed as : r= 2 s i n ( C ) c
->From this equality we easily get that Cos²(C)= 1-sin²(C)=1- r ² 1 3 ( 2 r − 1 3 )
We use the law of cosine knowing the values of the a,b,c and cos(c) in terms of r :
->52(2r-13)=64(2r-16)+80(2r-20)-2ab.cos(C)
we sort the values and square both sides
->(92r-974)²=a²b².cos²(C)
Finally we get this equation :
->(92r-974)²=64(2r-16)80(2r-20) (1- r ² 1 3 ( 2 r − 1 3 ) )
We find several values for r, the valid one being r= 2 6 5
After Solving for r, we solve for a, b and c a=56 b=60 c=52
We use this formula to find the area : Area= 4 r a b c = 1344
Solve
a^2=4x(2r-x), b^2=4y(2r-y), c^2=4z(2r-z), t=[a(r-x)+b(r-y)+c(r-z)]/2, t=(abc)/(4r),
Here, a, b,c are sides of triangle, x=13, y=16 and z=20. “t” is area of the triangle.
Solve by WolframAlpha to get
a=52, b=56, c=60, r=65/2, t=1344
Answer=1344
R = (C^2 + 4 M^2)/(8 M) where M =20 ,16 &13 R= radius of the circle C = chord (sides of the triangle)
(a^2 + 4 * 16^2) / (8 * 16) = (b^2 + 4 * 20^2) / (8 * 20) = (c^2 + 4 * 13^2) / (8 * 13) solve for a^2 ,b^2 & c^2 implies a=56 , b = 60 and c = 52 and R = 32.5 Area = 1344
?? (a^2 + 4 * 16^2) / (8 * 16) = (b^2 + 4 * 20^2) / (8 * 20) = (c^2 + 4 * 13^2) / (8 * 13) are in fact only two equations for the three unknowns a^2, b^2 and c^2. Two equations are in general not enough to solve three unknowns. So it is not clear how a=56, b=60 and c=52 are obtained.
Carnot's Theorem tells us that ( R − v A ) + ( R − v B ) + ( R − v C ) = R + r , where R is the outradius and r the inradius, and hence we deduce that 2 R − r = 4 9 Standard results tell us that v A = R ( 1 − cos A ) = b c 2 R ( s − b ) ( s − c ) , with similar results for v B , v C , and hence v A v B v C = a 2 b 2 c 2 8 R 3 ( s − a ) 2 ( s − b ) 2 ( s − c ) 2 = s 2 a 2 b 2 c 2 8 R 3 Δ 4 = 1 6 s 2 R 2 Δ 2 8 R 3 Δ 4 = 2 s 2 R Δ 2 = 2 1 R r 2 where Δ = s ( s − a ) ( s − b ) ( s − c ) = 4 R a b c = r s is the area of the triangle and s its semiperimeter, so that R r 2 = 8 3 2 0 Thus we deduce that R ( 2 R − 4 9 ) 2 = 8 3 2 0 , so that R is one of 2 6 5 , 4 1 ( 3 3 + 6 5 ) and 4 1 ( 3 3 − 6 5 ) . Neither the second nor the third of these is possible, since they both imply that R < 1 3 = v C . Thus we deduce that R = 2 6 5 and therefore r = 1 6 .
It is now easy to calculate that cos A = 6 5 3 3 , cos B = 1 3 5 and cos C = 5 3 , so that a = 5 6 , b = 6 0 , c = 5 2 and hence s = 8 4 , so that Δ = r s = 1 3 4 4 .