Find Area of Circle
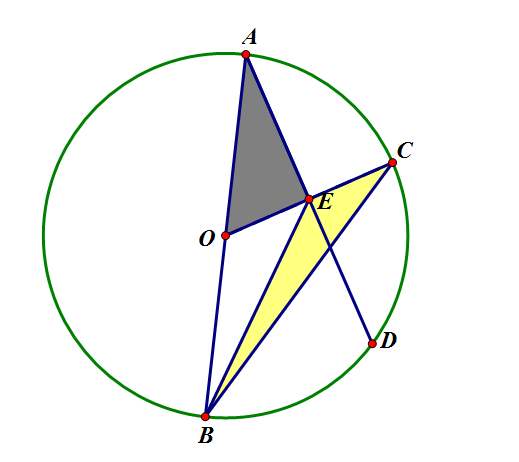 A
B
is the diameter of circle centered at
O
,
A
D
⊥
O
C
,
△
A
O
E
and
△
C
E
B
have the same area. The length of
A
D
is
1
, find the area of the circle.
A
B
is the diameter of circle centered at
O
,
A
D
⊥
O
C
,
△
A
O
E
and
△
C
E
B
have the same area. The length of
A
D
is
1
, find the area of the circle.
The answer is 1.0472.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
It would help if you removed the extra image space above and below the notebook :).
O A = O B
△ E A O = △ E O B = △ C E B
O E = E C = 2 1 O C = 2 1 O A
∠ O E A = 9 0 ∘
△ E A O is the special 30-60-90 triangle.
Since A D is a chord, and O C ⊥ A D , A E = E D = 2 1
O A = 3 1
The area is π r 2 = 3 π ≈ 1 . 0 4 7
In a circle, if a cord is perpendicular to the radius, the radius AND chord are both bisected.
So A E = 2 1 and let the radius be 2 x , so O E = x
Use the Pythagorean theorem: ( 2 1 ) 2 + x 2 = ( 2 x ) 2 and the radius is 3 1 , therefore the area is approximately 1 . 0 4 7
How EAO=EOB ? Here,OA=OB but how AE=EB , if it is right then AE is not equal to ED. So is it a suitable solution?
Let the radius of the circle be r
Since AB is a diameter
Then angle ADB = 90
Then OE is parallel to BD (because angle AEO = 90)
Since O is midpoint of AB
Then E is midpoint of AD
Then AE = 1/2
Area of triangle AEO = area of triangle BEO ... (equal bases and common height)
Then
Area of triangle BEC = area of triangle BEO
Then
OE = CE = r/2
In the right triangle AEO
r^2 = (r/2)^2 + (1/2)^2
Then
r^2 = 1/3
So , the area of the circle = (Pi) r^2 = 1.047
Nice way of proof.
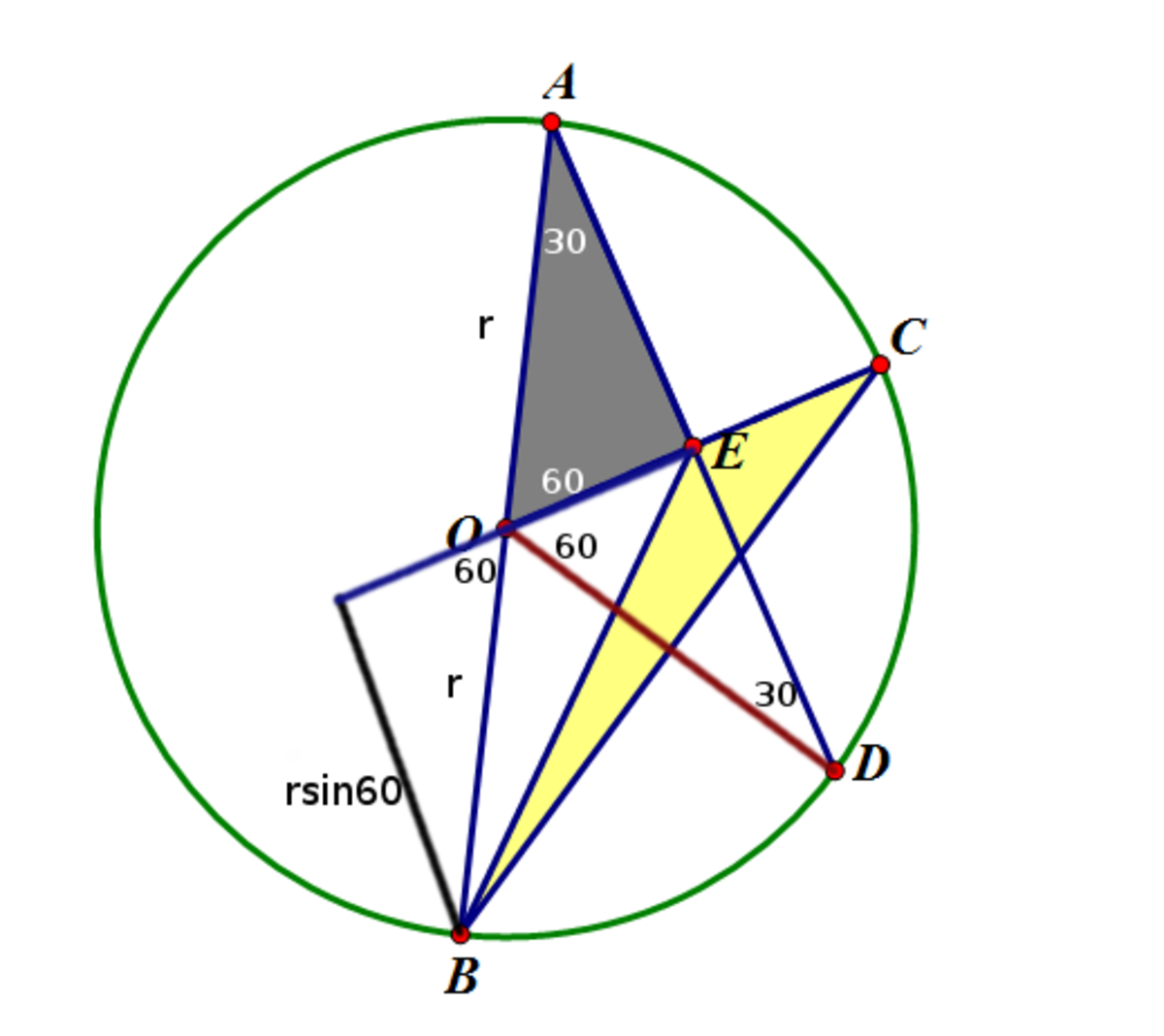 Let
∠
A
O
E
be
θ
Let
∠
A
O
E
be
θ
Area of △ A O E = Area of △ B E C
2 1 × r sin θ × r cos θ = 2 1 × ( r − r cos θ ) × r sin θ
⇒ cos θ = 1 − cos θ
cos θ = 2 1
θ = 6 0 ∘
⇒ ∠ O A D = 3 0 ∘
△ A O D is isosceles, so ∠ A O D = 1 2 0 ∘
Using cosine theorem on △ A O D
1 2 = r 2 + r 2 − 2 r 2 c o s 1 2 0 ∘ (AD=1)
⇒ r 2 = 3 1 a n d A r e a = 3 π
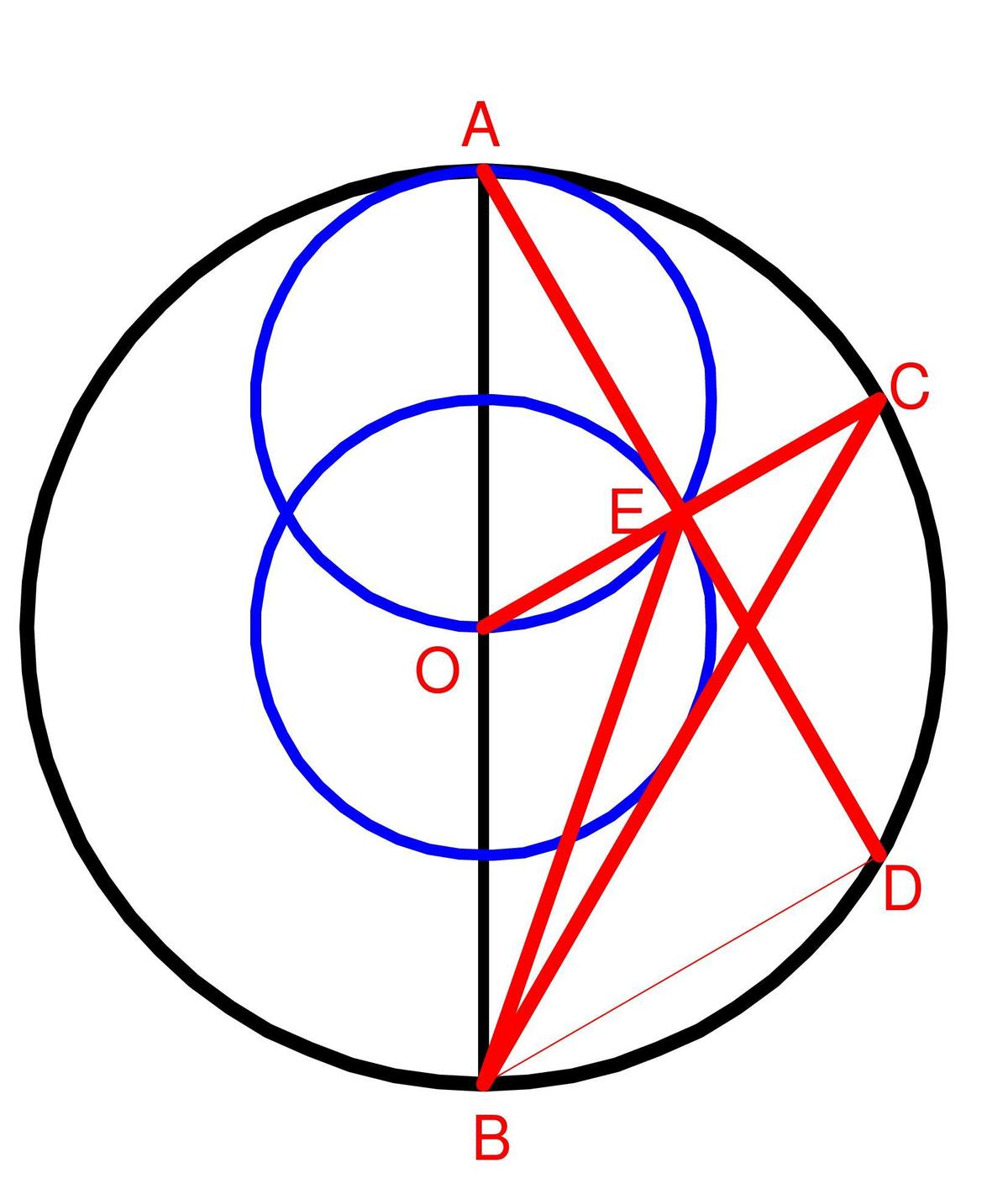 In my opinion the core of the problem is realizing that BE is the median of triangle BOC, since area of triangles AOE = OBE= BOC. As by hypothesis AD is perpendicular to OC, point E is in the intersection of the 2 auxiliaries circumferences as shown in drawing. AE equal half of AD and OE equals half of OA.
In my opinion the core of the problem is realizing that BE is the median of triangle BOC, since area of triangles AOE = OBE= BOC. As by hypothesis AD is perpendicular to OC, point E is in the intersection of the 2 auxiliaries circumferences as shown in drawing. AE equal half of AD and OE equals half of OA.
Therefore by Pythagoras OA = 1/sqrt{3}and the Area is Pi/3
I n △ AEO and BEO, base AO=BO, common hight. ∴ A r e a s a m e . ⟹ A r e a s o f △ B E O a n d B E C a r e s a m e a n d h a v e t h e c o m m o n h i g h t . ∴ b a s e s a r e e q u a l . ⟹ E i s m i d p o i n t o f O C . B u t O C = R , r a d i u s o f t h e c i r c l e . r a d i u s O C ⊥ c h o r d A D . ∴ E i s m i d p o i n t o f A D . C E = 2 1 ∗ R . A E = 2 1 . S o i n t h e c i r c l e 4 1 = A E 2 = ( 2 R − C E ) ∗ C E = ( 2 R − 2 1 ∗ R ) ∗ 2 1 ∗ R . ∴ 4 1 = 4 3 ∗ R 2 . ∴ A R E A o f t h e c i r c l e = 3 π = 1 . 0 4 7
Angle OAE=30 Degree,AE=0.5 ,FROM RIGHT TRIANGLE (OAE) GET RADUIES OF CIRCLE (OA)=0.577 , HENCE: CIRCLE AREA=1.04719 SQUARE UNITE
Angle OAE = 30 Degrees, but that should be proved!!
PLZ reply if you have any confusion