Find Area Of Shaded Portion
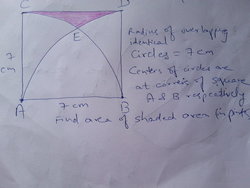 A square of side of 7 cm. The quarters of two identical circles of radius 7 cm overlap each other inside the square as shown. The centers of each circle are at corners of the square at points A and B respectively. Each of the circles passes through the center of the other.
A square of side of 7 cm. The quarters of two identical circles of radius 7 cm overlap each other inside the square as shown. The centers of each circle are at corners of the square at points A and B respectively. Each of the circles passes through the center of the other.
Find the area of the shaded portion in pink.
The answer is 2.11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
We did the same thing
how AEB is an equilateral triangle?
Log in to reply
AE = BE = radii of the two identical quarter circles = 7 cm = AB = Side of square = 7 cm. Therefore, Triangle AEB is equilateral.
by symmetry it should be an equilateral traingle and the solution is correct.
AE = BE = AB = 7cm
A good attempt......
When you round your answer, shouldn't it be 2 . 1 2 sq. cm?
I first draw the two overlapping circles as a whole and cut it from the center vertically. Then I drew a line conecting the center to the chord to make a triangle. I have noticed that if I cut the triangle horizontally You can have a 30-60-90 special triangle. so the central angle of the arc is 60 times to is equal to 120. then I get the area of the sector to be subtructed to the area of the tringle. then it is equal to the area of the polygon ABO on the drawing above.
Area of the sector is As = r^{2}(teta)/2 As = 7^{2}(120)/2 As = 49PI/3
Area of the triangle is: At = 1/2bh At = 1/2(7\sqrt{3})(3.5) At = (49\sqrt{3})/3
Area ABO: A = As - At A = 49PI/3 - (49\sqrt{3})/4 A = 30.095
Then I get the area of the quarter circle with radius is 7: Aq = PIr^{2}/4 Aq = PI7^{2}/4 Aq = 49PI/4
Then Area ABO is subtructed from Aq to get the area of polygon DBO. A of DBO = Aq - A of ABO A of DBO = 49PI/4 - 30.095 A of DBO = 8.3895
Then I made the Area of DBO doubled which is equivalent to 16.779 then I added the A of to get the area of the whole figure or the one that shaded black. A of figure = A of ABO + 16.779 A of figure = 30.095 + 16.779 A of figure = 46.874
Then the final step is get the area of the whole square of which is 7 by 7 then sibtruct the Area of the figure from it to get the area of the shaded pink. A pink = S^{2} - A of figure A pink = (7)^{2} - 46.874 A pink = 49 - 46.874 A pink = 2.126 or 2.13 is my final answer xD
Part AEB is not a triangle the sides are curved.
Integrate y=sqrt(49-x^2) from x= 0 to 3.5. The area comes to 23.437. Multiply it by 2 and deduct it from the square of 49 cm^2.
Integration is the best method.
deduct it from 49cm^2 **
deduct from 49cm^2 :-)
This is wrong
i did the same approach :)
Can you expand a little please
the place where both arcs are intersecting join them with the two centers (vertices of square)
the triangle formed will be an equilateral triangle as sides are all radius of arcs
there fore the sides will subtend an angle of 60 degree
therefore after subtracting area of triangle from area of sector we will get area of left out portion
double it and then add the area of triangle (mark this as 1st equation)
now add areas of two arcs which are given
now subtract the area which was marked as equation 1
NOW subtract the result you get from area of square.
i tried to explain as much as i could but i know without a visual it might be difficult to understand but i will try to give a visual ASAP
Till then keep following me!!
https://brilliant.org/discussions/thread/the-answer-to-the-problem-find-area-of-shaded-imag/
here is the pic
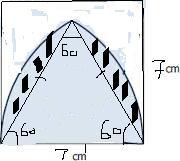 image
image
i tried my bestbut i could make only this much i hope it gives you some idea
Log in to reply
area of the desired region = area of the square - area covered by the two intersected identical quarter circles
1.Area of the square = 7*7 = 49 sq.cm
2.area covered by the two intersected identical quarter circles = (2* area of the quarter circle) - area of intersection
a.area of the quarter circle = (pi * r^2)/4 = 154/4
b.area of intersection = (2* ((area of the circle/6) - area of the equilateral triangle formed in the above pic))+ area of the equilateral triangle formed in the above pic
i.area of the circle = pi * r^2 = (22/7) 7 7 = 154
ii.area of the equilateral triangle formed in the above pic = (sqrt(3)/4) *(7^2) = 21.2176
now from step i and ii, step b becomes area of intersection = (2*((154/6)-21.2176)) + 21.2176 = 30.1157
therefore, step 2 becomes area covered by the two intersected identical quarter circles = (2*154/4) - 30.1157 =46.8843
hence area of the desired region = 49 - 46.8843 = 2.1157 (approximately)
This is correct methodology to obtain the solution
<p>ABCD = 49</p>
<p>ABE = 49*1.73/4</p>
<p>ACE + DEB = 49*3.14/6</p>
<p>The pink area is ABCD - ABE - ACE - DEB = 2.11</p>
I used integration and solved for the shaded region...
49-(pi 7 7/12)-(pi 7 7/12)-(sqrt(3) 7 7/4)
I've just made and equilateral triangle with sides of 7 (triangle EAB) and two arcs with 30 degrees (CAE and DBE) and radius 7, found the area of the three and subtracted from 49, which is the area of the square
total area=49 area of 1/2 square=24.5 area under the curve AED=30 by ( integral sqrt(49-x^2) from 0 to 3.5 use principle of symmetry area under 1/2 the curve AED=15 area of 1/4 th of circle of r=7 is 38.465 area of half shaded region=24.5-(15+(38.465-30)=1.035 area of shaded region=1.035*2=2.07
From the point of intersection of the two circles near the center of the square, you can draw lines from to the center points of both circles, and since each of those lines are radii of the corresponding circles, they are 7 cm. The non shaded pieces you end up with are an equilateral triangle, and two identical slices of a circle.
After that step, the problem is much easier, if you drop a horizontal from the intersection of the circles you end up with two 30-60-90 triangles, and find that the height of that triangle is sqrt(3)3.5. Also, one notices that the remaining two circle slices are 30 degrees each.
Now that you have found have all the required dimensions of the non shaded portion you get the equation:
a = 49 - 1/2(sqrt(3)3.5 7) - (60/360 pi(49)) = ~2.11
DO IN 5 STEPS: 1.Write the equation of the first circle with centre at A: x^2+y^2=49 so that y=(49-x^2)^1/2 2.Then integrate the above (as dx) from 0 to 3.5 [Note- 3.5 is the intersection point of the curves of the circle] 3.Double your result. 4.Now you have all the area except the shaded region. 5.subtract from total area you have your answer.
We have two quarter circles intersecting inside the square to form a common area
Imagine two full circles from the right bottom and left bottom vertices of the square
Common area = 1/2 are of intersection of the two intersecting circles of radii 7 cm each whose centers are 7 cm apart
Area of 2 intersecting circles = 2* ( one third area of circle of radius = 7 cm - area of triangle whose one vertex is center of circle and other two are the points where the radius intersects the circumference of the one-third circle area. The angle between the radii is 120 degrees))
Area of shaded region = area of square - 2* area of quarter circles + area common to the two quarter circles
Final answer = 2.14 cm^2
O is the intersecting point of the line from E perpendicular to AB now the area of the circle is 153.86 cm2 the area ABE is one six the circle area i.e = 25.643333333 the triangle OBE area is 10.608 cm2 the quarter circle area is = 38.465 cm2 the area AOE = ABE-OBE = 25.643-10.608 AEC= quarter circle - 2{AOE} = 38.465-30.069 = 8.396 cm2 then CED = ABCD-2 AOE - 2 AEC = 49 - 30.069 - 16.792 = 2.139 final result = 2.139
Join AE and BE. You get an equilateral triangle AEB (side length = 7cm).
Angle CAB = Angle DBA = 90 degrees
Angle in equilateral triangle = 60 degrees. (Angle EAB = Angle EBA = Angle AEB)
Angle EAC = 30 degrees
Angle EBD = 30 degrees
Area of equilateral triangle = (sqrt(3)/4) a a, where a is the length of the side of triangle.
Area of triangle AEB = (sqrt(3)/4) 7 7 = 21.2176223927 sq.cm.
Area of sector = (n/360) pi r*r, where pi=22/7, r=radius of circle, n=angle made by sector with centre.
Here AEC and BED are sectors which make 30 degrees with centre of their respective circles.
Area of sector AEC = (30/360) (22/7) 7*7 = 12.8333333333 sq.cm.
Area of sector BED = (30/360) (22/7) 7*7 = 12.8333333333 sq.cm.
Area of square ABCD = a*a, where a is length of side
Area of square ABCD = 7*7 = 49 sq.cm.
Area of shaded area = Area of square ABCD - (Area of triangle AEB + Area of sector BED + Area of sector AEC)
Area of shaded area = 49 - (21.2176223927 + 12.8333333333 + 12.8333333333) = 2.1157109407 sq.cm.