A geometry problem by Aly Ahmed
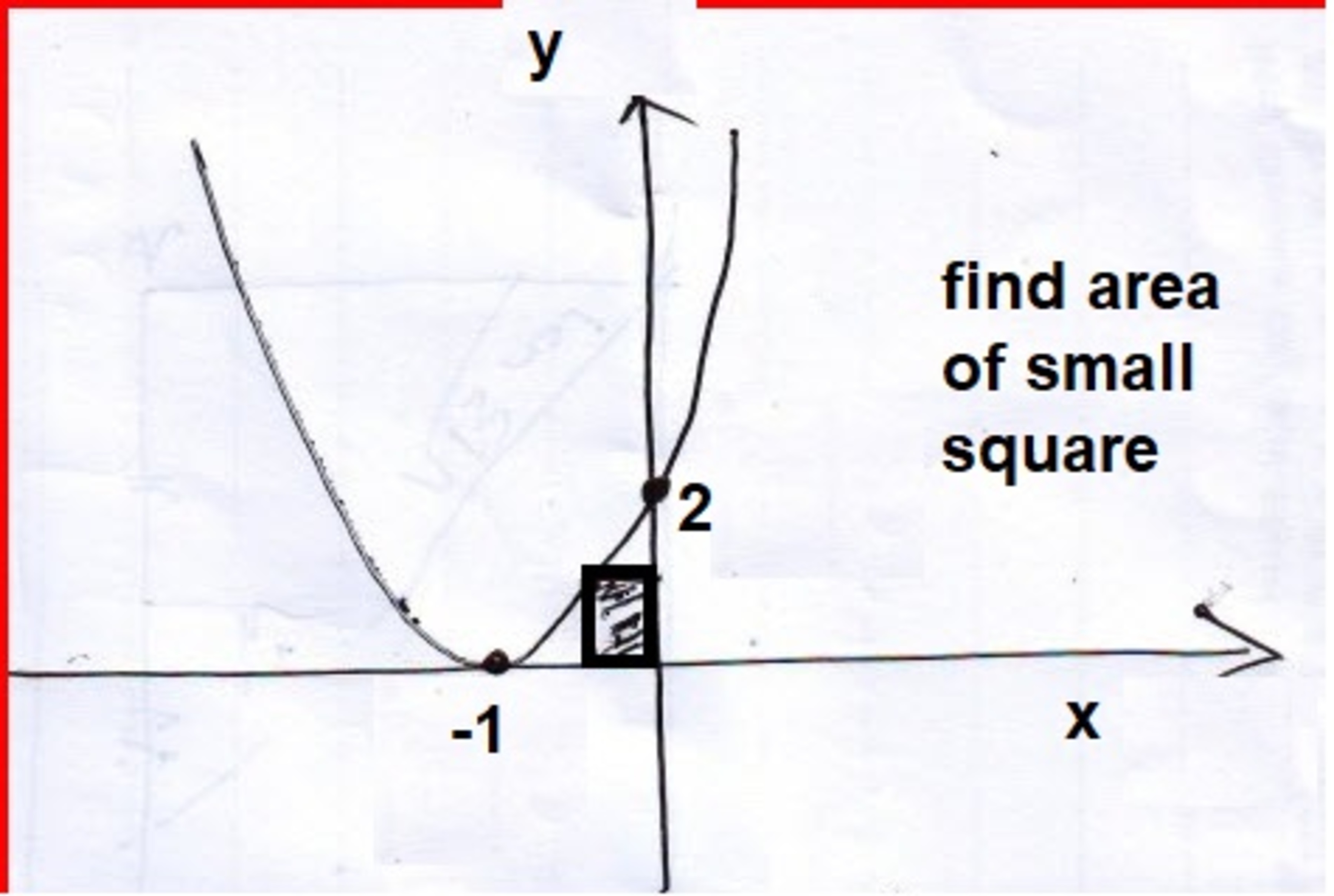
The curve above represents a parabola, it has an -intercept of -1 and -intercept of 2.
The answer is 0.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the parabola above be represented by y = 2 ( x + 1 ) 2 . Pick a point P ( x 0 , 0 ) for x 0 ∈ ( − 1 , 0 ) such that 2 ( 1 + x 0 ) 2 = − x 0 . Solving for x 0 yields:
− x 0 = 2 ( 1 + x 0 ) 2 ⇒ 0 = 2 x 0 2 + 5 x 0 + 2 ⇒ 0 = ( 2 x 0 + 1 ) ( x 0 + 2 ) ⇒ x 0 = − 2 1 , − 2 .
Since only − 1 < − 2 1 < 0 , this is the desired value we want. The square thus has an area of ( 2 1 ) 2 = 4 1 .