Find Buried Pirate Treasure

Captain Teaches Kidd, a fearsome and paranoid pirate of the 1600s, repeatedly buries all his treasure in a single secret spot on a remote uninhabited island.

On that island, there are two big trees, $A$ , and $B$ , which are 1050 paces apart. He has long relied on a bizarrely complicated way to locate point $D$ where his massive hoard is buried, which involves 4 men walking on 4 different paths, as follows:

• First, he has 2 men, one walking from point $A$ the other from point $B$ , more or less towards each other, until the man from $A$ has traveled 294 paces and the other from $B$ has traveled 392 paces, and they are now 490 paces apart. Then both change directions and the first man walks 455 more paces and the other walks 525 more paces before they both meet at point $C$ . Here, they erect a temporary marker.

• Next, he has 2 more men, one walking from point $A$ the other from point $B$ , until

• (Note: all values marked ${x}_{i}$ are missing and no longer known)

• the man from point $A$ has traveled ${x}_{1}$ paces to where he is at ${x}_{2}$ paces distant from the marker at point $C$ , thence he continues in a different direction until he has traveled 273 paces to where he at ${x}_{3}$ paces from the marker at point $C$ , while

• the man from point $B$ has traveled ${x}_{4}$ paces to where he is at ${x}_{5}$ paces distant from the marker at point $C$ , thence he continues in a different direction until he has traveled ${x}_{6}$ paces to where he at 364 paces from the marker at point $C$ , after which

• the man from point $A$ continues another ${x}_{7}$ paces in a new direction and the man from point $B$ continues another ${x}_{8}$ paces in a new direction until they both meet at point $D$ , where the treasure is buried.

Originally, Captain Teaches Kidd had all the figures written down in different places, which he never shows all at once to anybody, but---alas!---in some terrible battle at sea in which his ship was sunk, he lost his papers and was only able to remember some of the numbers as follows (crude map not drawn to scale, dark lines indicates the 4 different paths $AC, BC, AD, BD$ ).

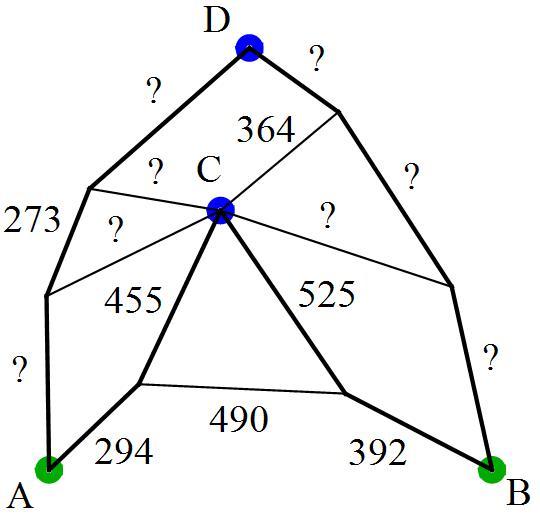
where the question marks indicate numbers that have been lost. Can you help him find his hoard again, by computing the straight-line distances $AD$ and $BD$ in paces?

Enter your answer as the sum $AD+BD$ .