Find EF

Geometry Level 2

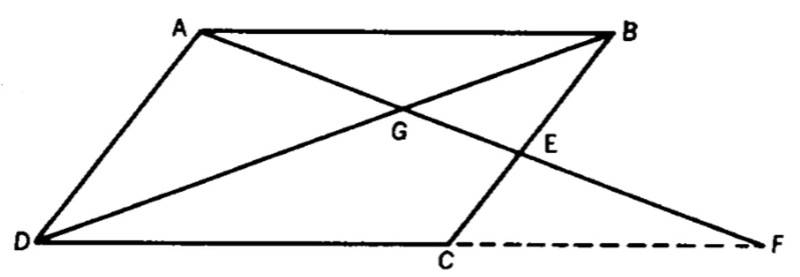
In the figure, $ABCD$ is a parallelogram, $AG = 6$ , and $GE=4$ . Find $EF$ .

The answer is 5.

2 solutions

Marvin Kalngan
May 1, 2020

Since, $\bigtriangleup FDG \sim \bigtriangleup ABG$ , $\dfrac{GF}{GA}=\dfrac{GD}{GB}$

And, $\bigtriangleup BGE \sim \bigtriangleup DGA$ , $\dfrac{GD}{GB}=\dfrac{GA}{GE}$

By transitivity, $\dfrac{GF}{GA}=\dfrac{GA}{GE}$

By substitution, $\dfrac{4+EF}{6}=\dfrac{6}{4}$

$4(4+EF)=6(6)$

$16+4EF=36$

$4EF=20$

$\color{#69047E}\large{\boxed{EF=5}}$

@Marvin Kalngan , I have provided a solution. You don't need to put ABCD, AG, and GE is \text{}. They are meant to be in italic as in thousand of questions in the Brilliant website. The regular non-italic form is reserved for function names. I have amended your problem question.

Chew-Seong Cheong - 1 year, 1 month ago

Chew-Seong Cheong
May 1, 2020

We note that $\triangle BEG$ and $\triangle ADG$ are similar. Therefore $\dfrac {BE}{AD} = \dfrac {AG}{GE} = \dfrac 64 = \dfrac 32$ . We also note that $\triangle ADF$ and $\triangle AEB$ are similar, therefore

$\begin{aligned} \frac {AF}{AE} & = \frac {BE}{AD} = \frac 32 \\ AF & = \frac 32 \times AE \\ AG+GE+EF & = \frac 32 (AG+GE) \\ \implies EF & = \frac 12 (AG+GE) = \frac 12 (6+4) = \boxed 5 \end{aligned}$

Find EF

The answer is 5.

2 solutions

0 pending reports