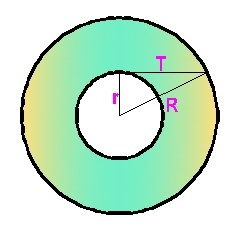
A Grey Ring

Consider this: hi So, the area of the shaded figure is $A=\pi{R}^{2}-\pi{r}^{2}$ $=\pi\times({R}^{2}-{r}^{2})$ Using Pythagoras Theorem, this is equals to $\pi\times({T}^{2})$ Since ${T}^{2}={R}^{2}-{r}^{2}$

This is a common MathCounts question. The fast way to do it is as follows. The question never states the radius of any of the circles, but it doesn't matter. Because it didn't state the radius, we can assume that the inner circle has radius $0$ . Thus, $T$ is the radius. If $T$ is the radius of a circle that is fully shaded in, then the area is $\pi * T^{2}$ , which is $\boxed {3.142*t^2}$ .

let radius of larger circle be R and smaller be r then, area of annulus =pi(R^2 - r^2) but , R^2 - r^2=T^2 and area=piT^2

We have two circles,Let r ans r1 be the radius of small and big circles.From centre if we draw lines to both points where T is shown we get right angled trianle.from this we find the area of Shaded region = pi r1 ^2 -pi( r1 ^2 - T ^2) = pi T^2 that is 3.142 xT^2 Ans K.K.GARG,India

first imagine the radius of small circle to be 'r' and big circle be 'R' using these find the areas we get a1=pi r^2 for small circle a2=pi R^2 for big circle. subtract the area of big circle by smaller one then we get A= pi (R^2-r^2)----------(1) [using pythagoras theorem] we get R^2=r^2 +t^2------------(2) then t^2=(R^2-r^2)---------------------(3) substitute in equation 1 we get A=pi (t^2)---------------------(4)

$By$ $pythagorean$ $theorem$ ,

$T^2=R^2 - r^2$

$A_{shaded}=A_{big circle}-A_{small circle}=πR^2-πr^2=π(R^2-r^2)=πT^2$

well... if one looks at the solution it is clear that the area can not be something like T^3 or T^0.5, so you are left with 2 options. I calculated it anyway, but please consider adding wiser solutions, otherwise it is too easy.

Let us assume that the radius of the Inner circle is r, and radius of outer circle is R.

From the centre let us draw an inner radius line segment touching the tip of tangent, and draw the outer radius line segment where tangent touches the outer circle. By properties of tangents the line segments representing T, r and R form a right angled triangle, giving:

R² = r² + t²

We get : t² = R² - r²

Now, the required area is given by : Are of outer circle - Area of inner circle : Area = πR² - πr² = π(R² - r²) = πt² = 3.142 x t²

Area = pi(bigger radius square-smaller radius square) By pythagoras theorem , t^2=R^2 - r^2 Area=pi * t^2

This is a good question and an ow some relation.. A triangle satisfying Pythagoras Theorem is in there...

as R= 2r t= sqrt (R^2- r^2 ) , t=1.732 * r , area shaded = piR^2 - PI r^2 = 3PI r^2 = 3.142*t^2