This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Assume B:(0,0), C:(9.0) and A:(a,b). Then, a²+b²=(2√10)² and (a-9)²+b²=(√85)² which makes A:(2,6),M:(1,3) & N:(5,3/2). This means KN² =(3-5)²+(0-3/2)²=25/4 or KN=5/2=2.5. As simple as that!
From the picture, we have cos α = 2 ⋅ 9 ⋅ 2 1 0 ( 2 1 0 ) 2 + 9 2 − ( 8 5 ) 2 = 1 0 1
Then, M C 2 = 9 2 + ( 1 0 ) 2 − 2 ⋅ 9 ⋅ 1 0 cos α = 9 1 − 1 8 1 0 1 0 1 = 9 1 − 1 8 = 7 3
Half the length, N C = 2 1 M C = 2 7 3 , so N C 2 = 4 7 3 .
Finding expression for β : cos β K N 2 ∴ K N = 2 ⋅ 9 ⋅ 7 3 9 2 + ( 7 3 ) 2 − ( 1 0 ) 2 = 1 8 7 3 1 4 4 = 7 3 8 = K C 2 + N C 2 − 2 K C ⋅ N C ⋅ cos β = 3 6 + 4 7 3 − 2 ⋅ 6 ⋅ 2 7 3 ⋅ 7 3 8 = 3 6 + 4 7 3 − 4 8 = 4 7 3 − 1 2 = 4 2 5 = 2 5
Use cos rule for ΔABC to find <A. cos A = (40+85-81)/(4√850) = 11/√850 , A=67.8. Use sin rule to find <C, 9/sinA = (2√10)/sinC , C = 40.6 Use sin rule for ΔAMC to find NC=x. 4x^2 = 95 - 2√850 . 11/√850 , x = 4.272. Use cos rule for ΔKNC to find KN. KN^2 = 36 + (73/4) cos 20.3. KN=2.48
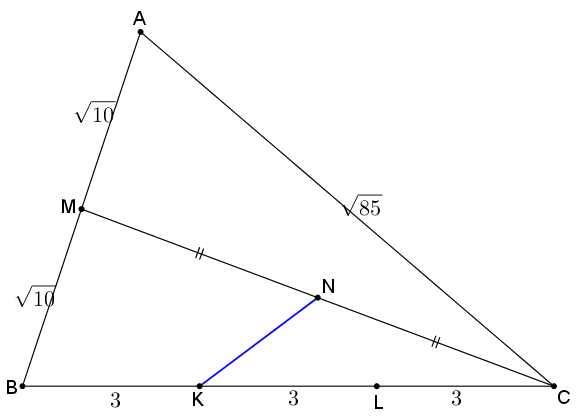
Extend B C and let the other end point be E , where B E = 3.
Connect E M , M K , and N L . Let N L = a , N K = b .
C L = L K = 3 . . . ( 1 )
C N = N M . . . ( 2 )
C K = K M = 6 . . . ( 3 )
From ( 1 ) ( 2 ) we know that M K = 2 a
From ( 2 ) ( 3 ) we know that E M = 2 b
According to Apollonius's Theorem:
C A 2 + C B 2 = 2( C M 2 + A M 2 )
8 5 + 8 1 = 2 ( C M 2 + 1 0 )
C M = 7 3
C N = 2 7 3
N K 2 + N C 2 = 2( N L 2 + K L 2 )
b 2 + 4 7 3 = 2 a 2 + 1 8 ⇒ 2 a 2 − b 2 = 4 1 . . . ( 4 )
E M 2 + M K 2 = 2( M B 2 + B E 2 )
4 b 2 + 4 a 2 = 3 8 . . . ( 5 )
After doing ( 5 ) − ( 4 ) × 2 we get:
6 b 2 = 2 7 5
b 2 = 4 2 5 ⇒ b = 2 5 = 2 . 5