Find Length II
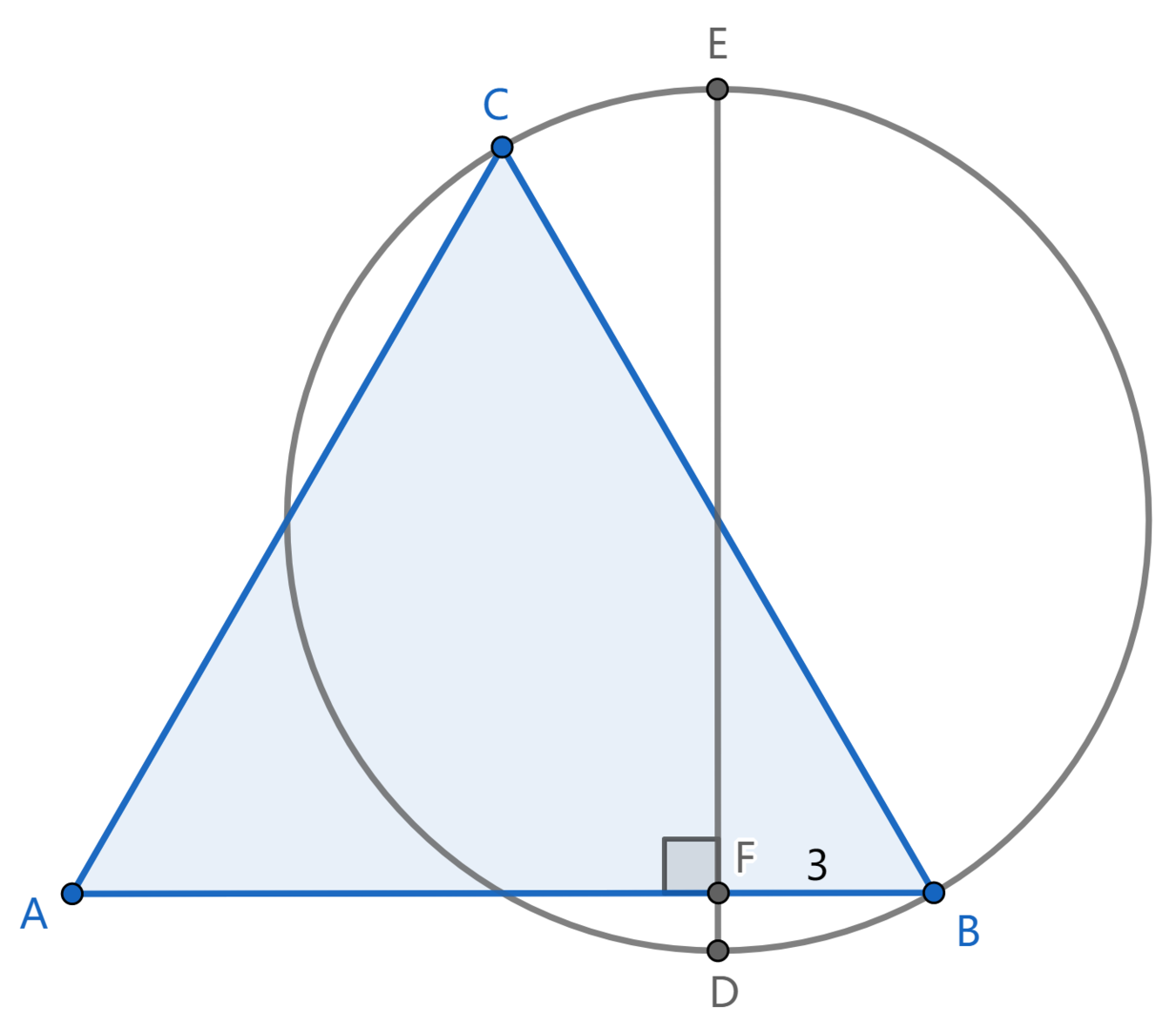 In equilateral triangle
A
B
C
,
B
and
C
lie on a circle, side
A
B
is perpendicular to the diameter of the circle
D
E
with foot
F
.
If the radius of the circle is
6
and
B
F
=
3
,
find the side length of triangle
A
B
C
.
In equilateral triangle
A
B
C
,
B
and
C
lie on a circle, side
A
B
is perpendicular to the diameter of the circle
D
E
with foot
F
.
If the radius of the circle is
6
and
B
F
=
3
,
find the side length of triangle
A
B
C
.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let D E cross B C at X .
Triangle B X F is a ( 6 0 ∗ , 3 0 ∗ , 9 0 ∗ ) triangle, so ∣ B X ∣ = 6 . Hence B X is a radius, B C is a diameter, and the side length is 1 2 .
Mark intersection of CB and ED as O.
O B = c o s ( 6 0 ) F B = 2 1 3 = 6
Since OB = R = 6, than O must be the center of the circle. B C = 2 R
A B = B C = A C
B C = 2 ∗ 6 = 1 2
Nice problem!
How do you know that the intersection point of C B and E D is the center of the circle?
Log in to reply
As OB equals radius, it must imply that interception is in the center.
Let G be the intersection of A B with the circumference and H to the intersection between E D and B C . As G F ≅ F B , △ F B H is equilateral of side lenght 6 , the same as the radius, then B C is diameter and its lenght is 1 2
Let the center of the circle be the origin O ( 0 , 0 ) . Then the equation of the circle is x 2 + y 2 = 3 6 . The y -coordinate of B is given by 3 2 + y B 2 = 3 6 ⟹ y B = − 3 6 − 9 = − 3 3 . The equation of chord B C is given by:
x − 3 y + 3 3 y + 3 3 ⟹ y = − tan 6 0 ∘ = − 3 = 3 3 − 3 x = − 3 x
Since the y -intercept of chord B C is 0, this means that it passes through the origin O ( 0 , 0 ) or the center of the circle. Therefore B C , which is a side of equilateral △ A B C , is a diameter of the circle and has a length of 1 2 .