Find Length of Hypotenuse
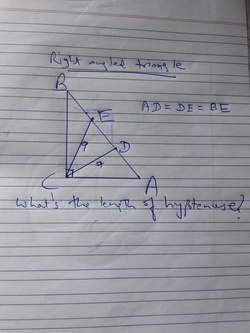Right angled triangle BCA. The points D and E lie on the hypotenuse such that AD= DE=EB.
Also CD= 7, CE=9
What is the length of the hypotenuse AB?
The answer is 15.297.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Oh! Just forgot to multiply by 9 ! A blunder!
Why FE=CH ?
Log in to reply
Hypotenuse is trisected and so are the sides. Ratio remains same.
Let a & b = BC ?
Actually, using Stuwarts theorem is quite simple too. Let B E = D E = D A = 2 u . By Stuwarts theorem, we get: 2 4 u 2 + 2 4 3 = A C 2 + 2 B C 2 . And 2 4 u 2 + 1 4 7 = 2 A C 2 + B C 2 . Adding the 2 equations gives: A C 2 + B C 2 = 1 6 u 2 + 1 3 0 . However, A C 2 + B C 2 = 3 6 u 2 . So u 2 = 1 3 / 2 . And 6 u = 1 5 . 2 9 7 .
let a = BC, b = AC
Add points F and G on BC such that BF= FG= GC
Add points H and I on CA such that CH= HI=IA.
Now one can see that FE = CH. But that means that CE^2 = EF^2 + FC^2, and thus
81= {(1/3) a} ^2 + {(2/3) b}^2
a^2+ 4b^2= 729. -------- 1
In the same way DC^2 = CI^2 + ID^2, and thus
49= {(1/3) b} ^2 + {(2/3) a}^2
b^2+ 4a^2= 441-------- 2
Adding [1] and [2] gives that
5a^2+ 5b^2= 1170
a^2+b^2= 234
So the hypotenuse must be sqrt (234).= 15.297