Find Length
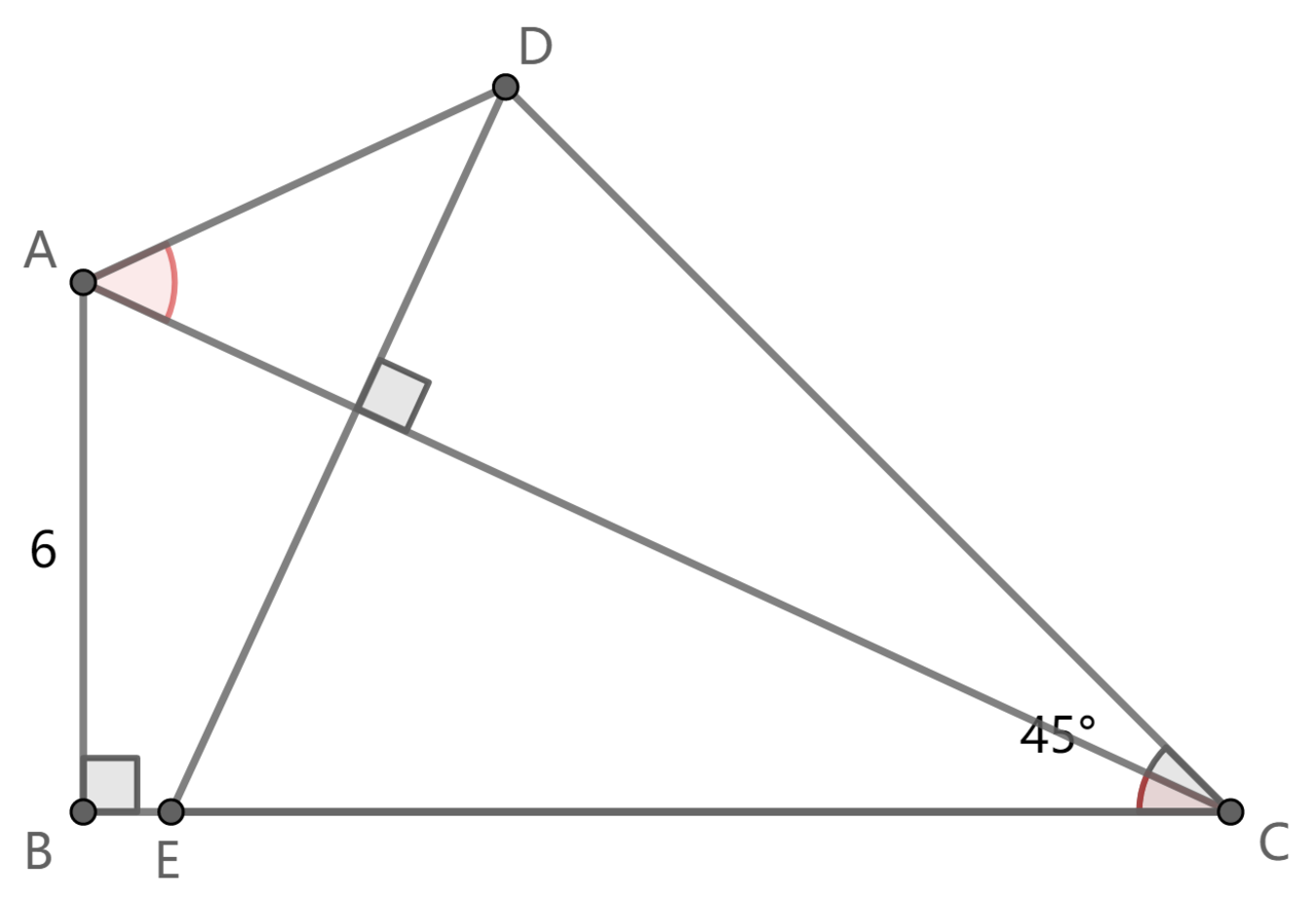
In quadrilateral A B C D , A B = 6 , ∠ A B C = 9 0 ∘ , ∠ B C D = 4 5 ∘ and ∠ C A D = 2 ∠ A C B . If D E is perpendicular to A C with E on side B C , find the length of C E .
Bonus: Solve it without trigonometry.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
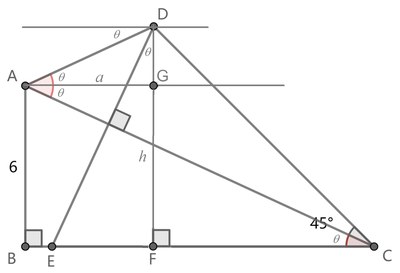
Let ∠ A C B = θ . Drop a altitude from D to B C and draw two straight lines parallel to B C through A and D . We note that ∠ D A G = ∠ E D F = θ . Since △ C D F is isosceles, D F = C F ; let their length be h . Then we have:
⎩ ⎨ ⎧ D F = D G + G F C F = B C − B F ⟹ h = a tan θ + 6 ⟹ h = tan θ 6 − a . . . ( 1 ) . . . ( 2 ) where A G = B F = a
From ( 1 ) + tan θ × ( 2 ) : h + h tan θ = 1 2 ⟹ h = 1 + tan θ 1 2
Now C E = C F + E F = h + h tan θ = 1 + tan θ 1 2 × ( 1 + tan θ ) = 1 2 .
Place the diagram on a coordinate system so that B is at the origin, C is on the x -axis, and A is on the y -axis. Let θ = ∠ A C B .
By trigonometry on △ A B C , B C = tan θ 6 .
Line C D has a slope of − 1 and an x -intercept (and a y -intercept) of tan θ 6 , so its equation is y = − x + tan θ 6 .
Line A D has a slope of tan ( ( 9 0 ° − θ ) + 2 θ − 9 0 ° ) = tan ( θ ) and a y -intercept of 6 , so its equation is y = ( tan θ ) x + 6 .
Lines A D and C D intersect at D ( t , u ) , where t = tan θ ( 1 + tan θ ) 6 ( 1 − tan θ ) and u = 1 + tan θ 1 2 .
Line A C has a slope of tan ( 1 8 0 ° − θ ) = − tan θ .
Since D E ⊥ A C , D E has a slope of tan θ 1 , and since it goes through ( t , u ) , its equation is y = tan θ 1 ( x − t ) + u .
Solving 0 = tan θ 1 ( x − t ) + u gives x = tan θ 6 − 1 2 = B E .
Therefore, C E = B C − B E = tan θ 6 − ( tan θ 6 − 1 2 ) = 1 2 .
This solution is inspired by @Chew-Seong Cheong.
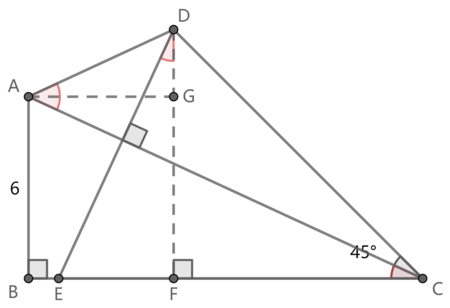 Drop an altitude from
D
to
B
C
and draw a straight line parallel to
B
C
through
A
.
⟹
⟹
⎩
⎪
⎪
⎨
⎪
⎪
⎧
△
A
D
G
∼
△
C
A
B
⟹
A
B
D
G
=
B
C
A
G
△
D
E
F
∼
△
C
A
B
⟹
A
B
E
F
=
B
C
D
F
A
B
D
G
+
E
F
=
B
C
A
G
+
D
F
=
B
C
B
F
+
C
F
=
1
C
E
=
C
F
+
E
F
=
D
F
+
E
F
=
F
G
+
D
G
+
E
F
=
A
B
+
A
B
=
1
2
.
Drop an altitude from
D
to
B
C
and draw a straight line parallel to
B
C
through
A
.
⟹
⟹
⎩
⎪
⎪
⎨
⎪
⎪
⎧
△
A
D
G
∼
△
C
A
B
⟹
A
B
D
G
=
B
C
A
G
△
D
E
F
∼
△
C
A
B
⟹
A
B
E
F
=
B
C
D
F
A
B
D
G
+
E
F
=
B
C
A
G
+
D
F
=
B
C
B
F
+
C
F
=
1
C
E
=
C
F
+
E
F
=
D
F
+
E
F
=
F
G
+
D
G
+
E
F
=
A
B
+
A
B
=
1
2
.
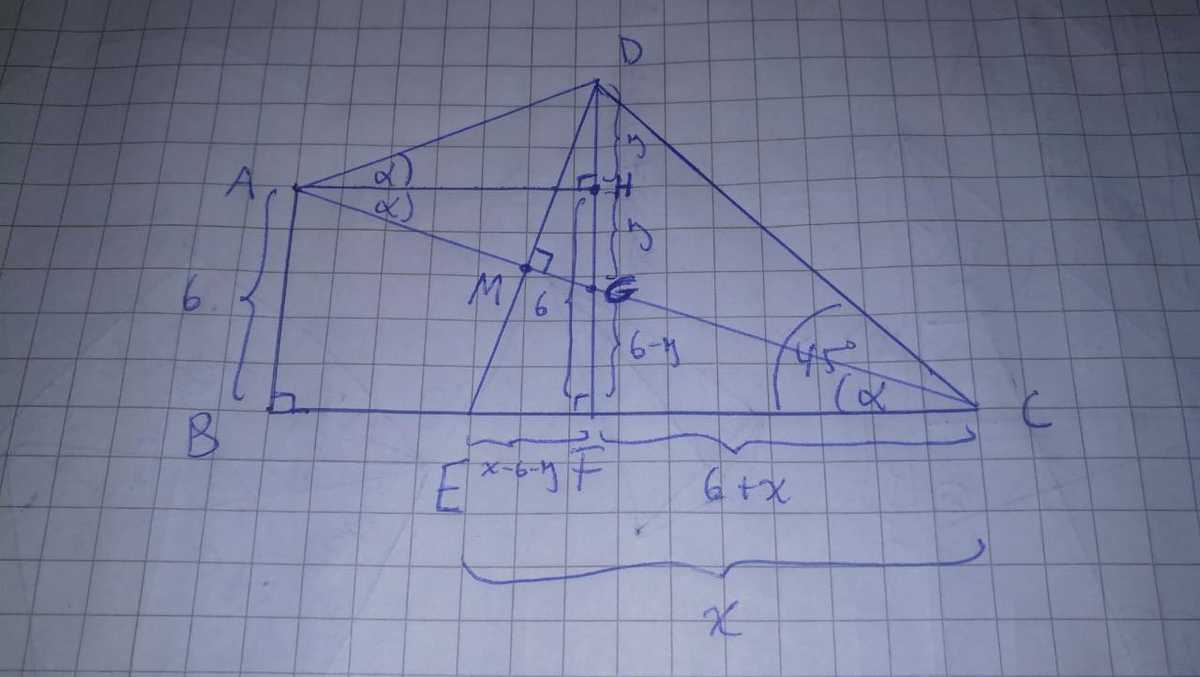
Let D H = y . As A H bisects ∠ D A G and A H ⊥ D G , D H ≅ H G . As H F = 6 , then F G = 6 − y . As △ D F C is isosceles, F C = 6 + x .
Then, as △ E F D ∼ △ G F C we have:
6 + y x − 6 − y = 6 + y 6 − y x = 1 2
Draw line AG // BC; CG ⊥ BC; extend AD so it intersects CD at F. Since ∠DAC = 2β, so FC = 2CG = 2AE = 12.
Since θ = 180° - 45° - a = β + 45°; θ’ = 2β + 45° - β = β + 45°, so θ = θ', ΔED’C = ΔFD’C, & EC = FC = 12