Find local max

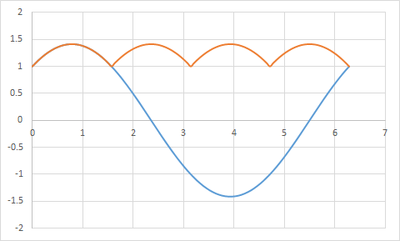
Local maximum of $\sin x+|\cos x|$ is obtained as $\sin x+\cos x=\sqrt 2 \sin (x+\frac{π}{4})$ in the range, for example, $[0, π]\cup [2π,3π]\cup... \cup [2nπ,(2n+1)π]\cup...$ . The maximum value is thus $\sqrt 2 \approx \boxed {1.4142}$ .

Oh, I missed the abs before $\sin x$ .

In this case, $0\leq |\sin x|+|\cos x|\leq \sqrt 2 \implies$ maximum value of the quantity is $\sqrt 2$ and the range is $[0,\sqrt 2 ]$ .

The blue curve is $\sin x + \cos x$ and the red curve is $|\sin x|+|\cos x|$ . Should the range of $|\sin x|+|\cos x|$ be $\sqrt 2-1 \approx 0.414$ ?