Find Max + Min
x 2 + y 2 − 1 4 x − 6 y = 6
Real values x and y satisfy the equation above. Find the sum of the maximum and minimum values of 3 x + 4 y .
The answer is 66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Can you please elaborate on “The linear function ... will attain its constrained extrema on opposite points on this circle, ... ”
Thanks
Log in to reply
As I mentioned, the values of f at opposite points add up to 2 f ( 7 , 3 ) = 6 6 , so, if one value is the maximum, then the other is the minimum. Let me spell this out: If f ( 7 + a , 3 + b ) ≥ f ( 7 + p , 3 + q ) for all points on the circle, then f ( 7 − a , 3 − b ) = 6 6 − f ( 7 + a , 3 + b ) ≤ 6 6 − f ( 7 + p , 3 + q ) = f ( 7 − p , 3 − q ) .
Thanks, I got it !! :)
x 2 + y 2 − 1 4 x − 6 y ( x − 7 ) 2 + ( y − 3 ) 2 = 6 = 6 + 4 9 + 9 = 6 4
⟹ ( x − 7 ) 2 + ( y − 3 ) 2 = 8 2 a circle with center at ( 7 , 3 ) and a radius of 8 . We can substitute
{ x − 7 = 8 cos θ y − 3 = 8 sin θ ⟹ x = 8 cos θ + 7 ⟹ y = 8 sin θ + 3
Then,
3 x + 4 y ⟹ max ( 3 x + 4 y ) ⟹ min ( 3 x + 4 y ) = 2 4 cos θ + 2 1 + 3 2 sin θ + 1 2 = 4 0 sin ( θ + tan − 1 4 3 ) + 3 3 = 4 0 + 3 3 = − 4 0 + 3 3 when sin ( θ + tan − 1 4 3 ) is maximum or = 1 when sin ( θ + tan − 1 4 3 ) is minimum or = − 1
Therefore max ( 3 x + 4 y ) + min ( 3 x + 4 y ) = 6 6 .
I think you are missing an inverse trig function in front of the ratio 3/4: θ + arctan ( 4 3 ) , rather than θ + 4 3 .
Of course, this does not affect the maximum or minimum values.
We look at it from a geometrical point of view .......
The equation just boils down to a equation of circle with center
(
7
,
3
)
and with radius
8
units .
Now it is evident that the maximum and minimum value
c
of
3
x
+
4
y
=
c
(
s
a
y
)
would be for the situations for which the line is tangent to this circle.
In other words we are looking for the maximum and minimum value of c for which the parallel straight lines become tangent to the circle.
Now we apply the fact that the perpendicular distance of the center from the line would be equal to the radius.......
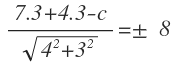
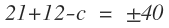
which gives the values of
c
=
−
7
and
7
3
.
Adding them we get our answer as
6
6
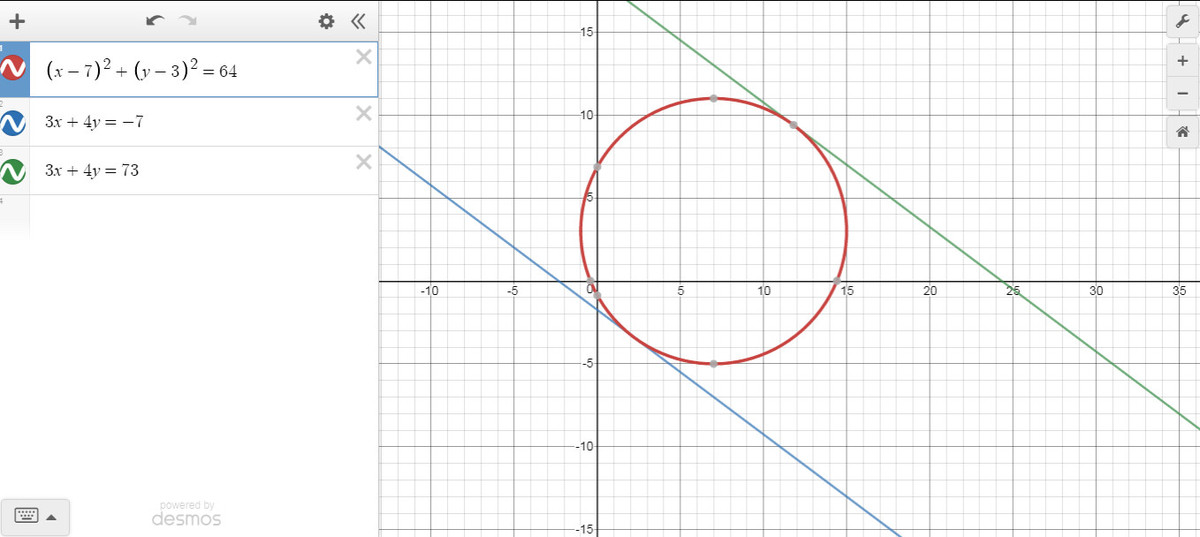
x 2 + y 2 − 1 4 x − 6 y = 6 ⟹ ( x − 7 ) 2 + ( y − 3 ) 2 = 8 2 ⟹ x = 7 + 8 cos ( θ ) , y = 3 + 8 sin ( θ ) ⟹ 3 x + 4 y = ( 2 1 + 2 4 cos ( θ ) ) + ( 1 2 + 3 2 sin ( θ ) ) = 3 3 + 2 4 2 sin ( θ + 4 π ) + 8 sin ( θ )
This value is maximum for θ = 4 π and minimum for θ = 4 − 3 π .
Therefore maximum value will be 3 3 + 2 4 2 + 4 2 = 3 3 + 2 8 2 and minimum will be 3 3 − 2 8 2 .
Hence the sum is 3 3 + 2 8 2 + 3 3 − 2 8 2 = 6 6 .
The equation x 2 + y 2 − 1 4 x − 6 y = 6 defines a circle centered at ( 7 , 3 ) . The linear function f ( x , y ) = 3 x + 4 y will attain its constrained extrema on opposite points on this circle, ( 7 + a , 3 + b ) and ( 7 − a , 3 − b ) , so that the sum of these two extrema is 2 f ( 7 , 3 ) = 6 6 .