Double triangles

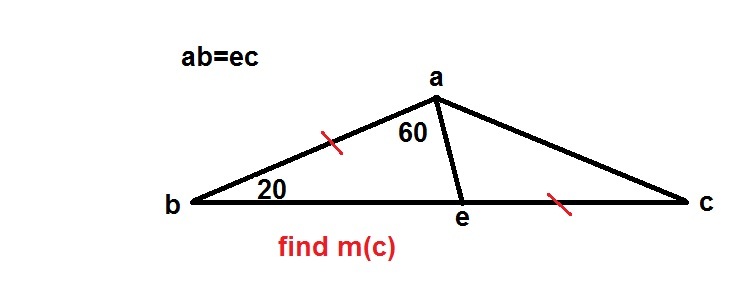
Note: The figure is confusing because $\angle AEB = 100^ \circ$ , but it looks acute.

The sum of the angles in a triangle = 180, therefore angle BEA = 100; angle AEC is supplementary and therefore = 80. Let angle c = x, then angle EAC = 180 - 80 - x = 100 - x.

Since EC and AB are equal in length, 'move' triangle ACE on top of triangle AEB, by constructing point $F$ such that $\triangle FAB \cong \triangle ACE$ .
Extend Notice that $\angle FBE = \angle FBA + \angle ABE = \angle AEC + \angle ABE= 100^\circ$ , $\angle AEB = 100^ \circ$ . If we extend AE and BF to intersect at G, then $EBG$ is an isosceles triangle with $GB = GE$ since that have the same base angles $80 ^ \circ$ .

Notice that $BF = AE$ by the congruent triangles, so $GF = GA$ giving us another set of isosceles triangles. Hence $80 ^ \circ = \angle BFA = \angle EAC$ and so $\angle ACB = 180 ^ \circ - \angle EAC - \angle AEC = 180 ^ \circ - 80^ \circ - 80^ \circ = 20^ \circ$ .

Construct a triangle congruent to ABE underneath line segment CE. This forms an isosceles trapezoid when combined with triangle AEC, and from there, it is apparent what the remaining angles in the triangle are.

While it's not as elegant as the solutions below, this can also be solved via "brute force" with the Law of Sines and some algebra...