Find my way out
1000 people have gathered for a unique competition. As shown, each participant has a very easy task of navigating a grid from start to finish, only walking upwards and rightwards. But there is one condition: no 2 people can choose the same pathway. If a competitor treads on a previously chosen way, he or she will be eliminated.
Below is a preview of a possible path. If were successful among the first participants, what is the chance in % that the runner completes his task?
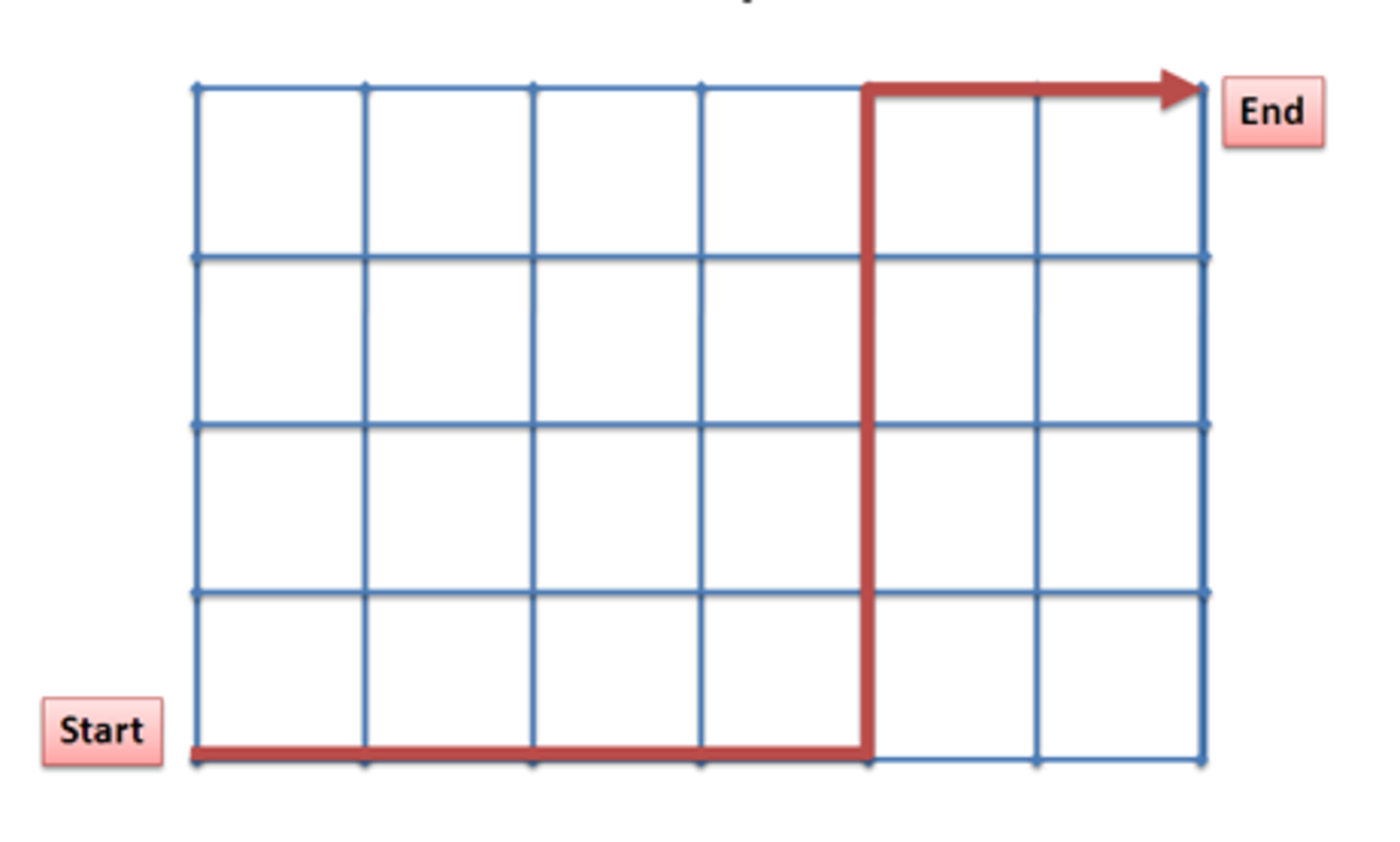
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The no of ways one can navigate a grid can be used by the basic theories of permutation.
A person has to take 6 rights and 4 ups in order to complete the grid Thus no of ways of navigating the grid is aranging 6 right and 4 ups
ie, 10! / (6!*4!)=210
given that 63 people were sucessful thus there are still 210-63 ways left =147 ways left
the possibility that the next person is sucessful is given by (147/210)*100
= 70%