Find B C in this triangle
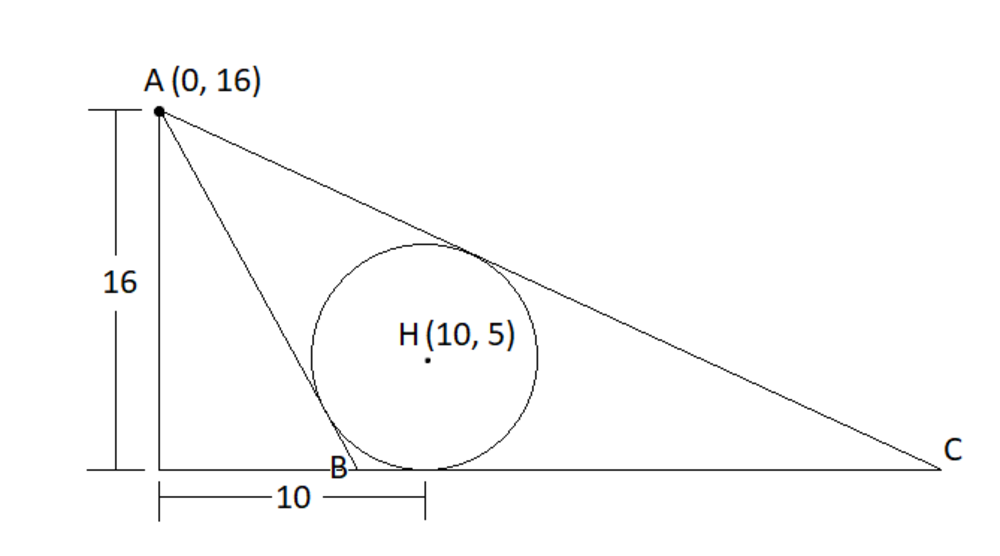
A circle of radius 5 is centered at point H ( 1 0 , 5 ) . Tangents from point A ( 0 , 1 6 ) are drawn to the circle as shown in the above diagram. They intersect the x -axis at points B and C . Find the distance d = B C , and enter the value of 3 d .
The answer is 70.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Very nice solution. But could you elaborate more on how to solve the three equations, to obtain the values of the slope m ?
Log in to reply
I did it by a series of substitutions.
Substituting y = m x + 1 6 into ( x − 1 0 ) 2 + ( y − 5 ) 2 = 2 5 gives ( x − 1 0 ) 2 + ( m x + 1 1 ) 2 = 2 5 , and into 2 ( x − 1 0 ) + 2 ( y − 5 ) m = 0 gives 2 ( x − 1 0 ) + 2 ( m x + 1 1 ) m = 0 .
Solving 2 ( x − 1 0 ) + 2 ( m x + 1 1 ) m = 0 for x gives x = m 2 + 1 1 0 − 1 1 m , and substituting that into ( x − 1 0 ) 2 + ( m x + 1 1 ) 2 = 2 5 gives ( m 2 + 1 1 0 − 1 1 m − 1 0 ) 2 + ( m ⋅ m 2 + 1 1 0 − 1 1 m + 1 1 ) 2 = 2 5 .
( m 2 + 1 1 0 − 1 1 m − 1 0 ) 2 + ( m ⋅ m 2 + 1 1 0 − 1 1 m + 1 1 ) 2 = 2 5
⟹ ( m 2 + 1 − 1 0 m 2 − 1 1 m ) 2 + ( m 2 + 1 1 0 m − 1 1 ) 2 = 2 5
⟹ ( m 2 + 1 ) 2 ( m 2 + 1 ) ( 1 0 m + 1 1 ) 2 = 2 5
⟹ m 2 + 1 ( 1 0 m + 1 1 ) 2 = 2 5
⟹ 1 0 0 m 2 + 2 2 0 m + 1 2 1 = 2 5 m 2 + 2 5
⟹ 7 5 m 2 + 2 2 0 m + 9 6 = 0
⟹ ( 5 m + 1 2 ) ( 1 5 m + 8 ) = 0
so m = − 5 1 2 and m = − 1 5 8 .
Log in to reply
Thank you for a very clear presentation of the solution method.
Let the tangent AB intersect the circle at point P, tangent BC intersect at Q, and tangent AC intersect at R. Furthermore, let the origin be O. Before reading on, draw a diagram with these labelled points first!
Firstly, find AP. A H 2 = ( 0 − 1 0 ) 2 + ( 1 6 − 5 ) 2 = 2 2 1 , and P H 2 = 5 2 = 2 5 (radius), hence A P = A H 2 − P H 2 = 2 2 1 − 2 5 = 1 4 .
Since tangents from the same point have the same length, BP = BQ = x, so OB = OQ - BQ = 10 - x, and AB = AP + PB = 14 + x. Thus by Pythagoras, 1 6 2 + ( 1 0 − x ) 2 = ( 1 4 + x ) 2 ⇒ 2 5 6 + 1 0 0 − 2 0 x + x 2 = 1 9 6 + 2 8 x + x 2 ⇒ x = 3 1 0 .
Then using the property again, RC = QC = a, so OC = OQ + QC = 10 + a, and AC = AR + RC = 14 + a (AP = AR). Therefore 1 6 + ( 1 0 + a ) 2 = ( 1 4 + a ) 2 ⇒ 2 5 6 + 1 0 0 + 2 0 a + a 2 = 1 9 6 + 2 8 a + a 2 ⇒ a = 2 0 .
Thus BC = BQ + QC = x + a, so 3 B C = 3 ( 2 0 + 3 1 0 ) = 7 0 .
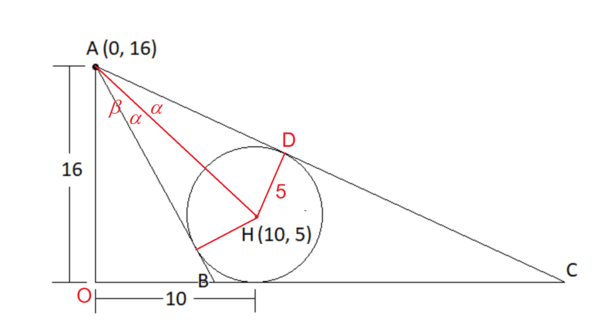
Let the origin be O ( 0 , 0 ) , ∠ C A H = ∠ B A H = α and ∠ O A H = β . Then sin α = A H H D = ( 1 0 − 0 ) 2 + ( 5 − 1 6 ) 2 5 = 2 2 1 5 ⟹ tan α = 1 4 5 . And tan β = 1 6 − 5 1 0 = 1 1 1 0 . Then we have:
O C O B d ⟹ 3 d = A O ⋅ tan ∠ C A O = 1 6 ⋅ tan ( β + α ) = 1 6 ⋅ 1 − 1 1 1 0 1 4 5 1 1 1 0 + 1 4 5 = 3 0 = A O ⋅ tan ∠ B A O = 1 6 ⋅ tan ( β − α ) = 1 6 ⋅ 1 + 1 1 1 0 1 4 5 1 1 1 0 − 1 4 5 = 3 2 0 = O C − O B = 3 7 0 = 7 0
A brilliant geometric solution. Thanks for sharing.
First, we'll find the distance A H
A H = 1 0 2 + 1 1 2 = 2 2 1
Then the two tangents A B and A C are separated by an angle 2 θ , where
θ = sin − 1 ( 2 2 1 5 )
from which, cos θ = 1 − 2 2 1 2 5 = 2 2 1 1 9 6
Here is the key to this problem. The vector extending from point A to a point on either of the two tangents makes an angle θ with the vector A H . Let r = ( x , y ) be any point on either of the two tangents, then the above statement implies that,
( r − A ) ⋅ ∣ A H ∣ A H = cos θ ∣ r − A ∣
Now, the vector A H = ( 1 0 , − 1 1 ) = [ 1 0 , − 1 1 ] T , so in matrix notation, the above dot product is written as,
( r − A ) T [ 1 0 − 1 1 ] = 1 9 6 ∣ r − A ∣
Squaring,
( r − A ) T [ 1 0 0 − 1 1 0 − 1 1 0 1 2 1 ] ( r − A ) = 1 9 6 ( r − A ) T ( r − A )
subtracting the right hand side from the left hand side, we obtain,
( r − A ) T [ − 9 6 − 1 1 0 − 1 1 0 − 7 5 ] ( r − A ) = 0
this is the equation of the two tangents.
Plugging in y = 0 yields the x-coordinates of points B and C :
[ x , − 1 6 ] T [ − 9 6 − 1 1 0 − 1 1 0 − 7 5 ] [ x − 1 6 ] = 0
Expanding this quadratic form, we obtain,
− 9 6 x 2 − 2 2 0 ( − 1 6 ) ( x ) − 7 5 ( − 1 6 ) 2 = 0
which simplifies to,
3 x 2 − 1 1 0 x + 6 0 0 = 0
and this factors to,
( 3 x − 2 0 ) ( x − 3 0 ) = 0
Hence, B = ( 3 2 0 , 0 ) and C = ( 3 0 , 0 )
and d = B C = 3 0 − 3 2 0 = 3 7 0
Hence, 3 d = 7 0
Circle H has an equation of ( x − 1 0 ) 2 + ( y − 5 ) 2 = 2 5 , and using implicit differentiation on this equation with m = d x d y we can obtain 2 ( x − 1 0 ) + 2 ( y − 5 ) m = 0 . Also, a tangent point on A B and a tangent point on A C to this circle will both fit the equation y = m x + 1 6 .
These three equations solve to m = − 5 1 2 and m = − 1 5 8 , so A B has an equation of y = − 5 1 2 x + 1 6 and A C has an equation of y = − 1 5 8 x + 1 6 .
Setting y = 0 on both of these equations and solving gives B ( 3 2 0 , 0 ) and C ( 3 0 , 0 ) , so that d = B C = 3 0 − 3 2 0 = 3 7 0 , and 3 d = 7 0 .