Sixth Degree Equation

The funtion is $x+(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)$

For this problem we cannot put directly the value as $p(7) = 7$ . It is a wrong method.

$p(x) = x$ for $x = 1,2,3,4,5,6 \implies p(x) - x = 0$

Let $q(x) = p(x) - x \implies p(x) = q(x) + x$

For x = 1 $\rightarrow q(1) = p(1) - 1 = 0 \implies \text{1 is a root of q(x)}$

For x = 2 $\rightarrow q(2) = p(2) - 2 = 0 \implies \text{2 is a root of q(x)}$

$\vdots$

For x = 6 $\rightarrow q(6) = p(6) - 6 = 0 \implies \text{6 is a root of q(x)}$

So, $\text{1, 2, 3, 4, 5, 6, are roots of q(x)}$ so we can write $q(x)$ as :

$q(x) = (x - 1)(x - 2)(x - 3)(x - 4)(x - 5)(x - 6)$

So, $p(x) = x + (x - 1)(x - 2)(x - 3)(x - 4)(x - 5)(x - 6)$

Now, $p(7) = 7 + (7 - 1)(7 - 2)(7 - 3)(7 - 4)(7 - 5)(7 - 6)$

$\implies p(7) = 7 + 6 \times 5 \times 4 \times 3 \times 2 \times 1$

Therefore, $p(x) = 7 + 720$

$\implies \color{#20A900}\text{p(x) = 727}$

You should ask for a monic polynomial of degree 6 with all integer coefficients. Otherwise, there's an infinity of monic polynomials of degree 6 with rational but not necessarily all integer coefficients.

The method of differences is mentioned elsewhere, but actually provides an even shorter solution.

We construct the difference table, using the given values and putting $k=p(7)$ :

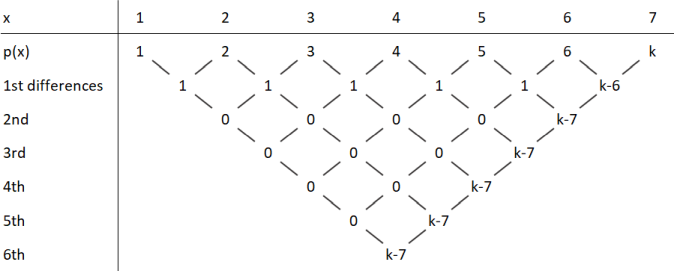
Since $p$ is monic and has degree $6$ , and the $x$ -values in the top row increase by $1$ at each step, the $6^{th}$ differences will all be $6!=720$ . In particular, $k-7=720$ , or $p(7)=\boxed{727}$

Since the polynomial is monic, we have the term $x^6$ given. This alone would result in the following values

$\begin{array}{ccc} x & x^6 & x^6-x \\ 1 & 1 & 0 \\ 2 & 64 & 62 \\ 3 & 729 & 726 \\ 4 & 4096 & 4092 \\ 5 & 15625 & 15620 \\ 6 & 46656 & 46650 \end{array}$

This means we are looking for a fifth degree polynomial $q(x)$ that corrects the values. It satisfies $p(x)=x^6-q(x)$ . We can find this polynomial's next value by the method of finite differences .

$\begin{array}{cccccc} x & q(x) & D_1 & D_2 & D_3 & D_4 & D_5 \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ {\color{#D61F06}7} \end{array} & \begin{array}{c} 0 \\ 62 \\ 726 \\ 4092 \\ 15620 \\ 46650 \\ {\color{#D61F06}116922} \end{array} & \begin{array}{c} 62 \\ 664 \\ 3366 \\ 11528 \\ 31030 \\ {\color{#3D99F6}70272} \end{array} & \begin{array}{c} 602 \\ 2702 \\ 8162 \\ 19502 \\ {\color{#3D99F6}39242} \end{array} & \begin{array}{c} 2100 \\ 5460 \\ 11340 \\ {\color{#3D99F6}19740} \end{array} & \begin{array}{c} 3360 \\ 5880 \\ {\color{#3D99F6}8400} \end{array} & \begin{array}{c} 2520 \\ {\color{#3D99F6}2520} \end{array} \end{array}$

We get that this fifth degree correction term gives $q(7)=116922$ for $x=7$ .

$p(x)=x^6-q(x) \Rightarrow p(7)=117649-116922 = \boxed{727}$