Find radius of circle

Geometry Level 3

Two circles of unit radii touch each other and each of them touches internally a circle of radius two,as shown in figure. The radius of the circle which touches all three circles is __________ \text{\_\_\_\_\_\_\_\_\_\_} .


The answer is 0.66.

Ankit Alria by ANKIT ALRIA , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Satyabrata Dash
Feb 29, 2016

6 Helpful 0 Interesting 0 Brilliant 0 Confused

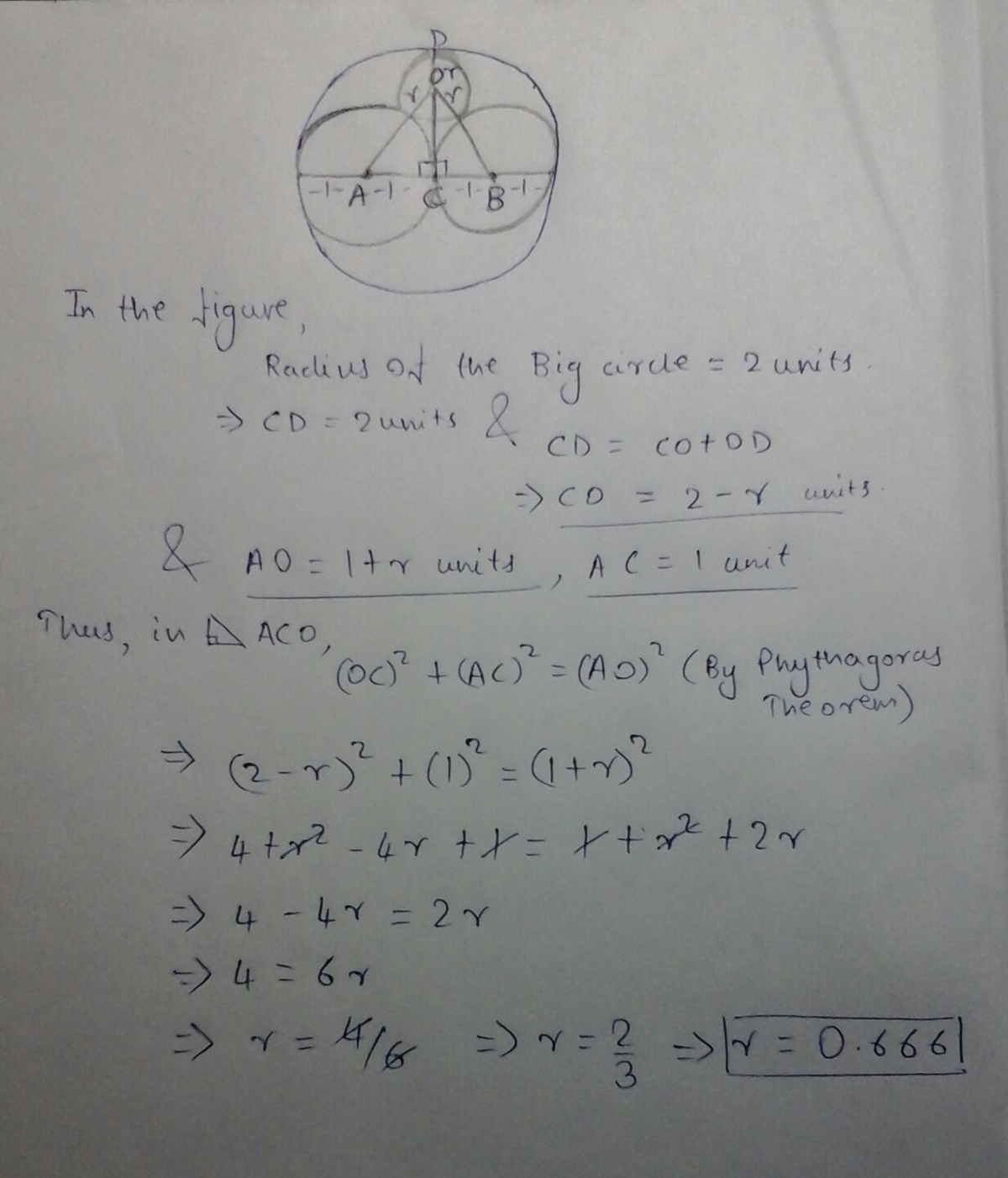
I used the same method....

Hritesh Mourya - 5 years, 3 months ago

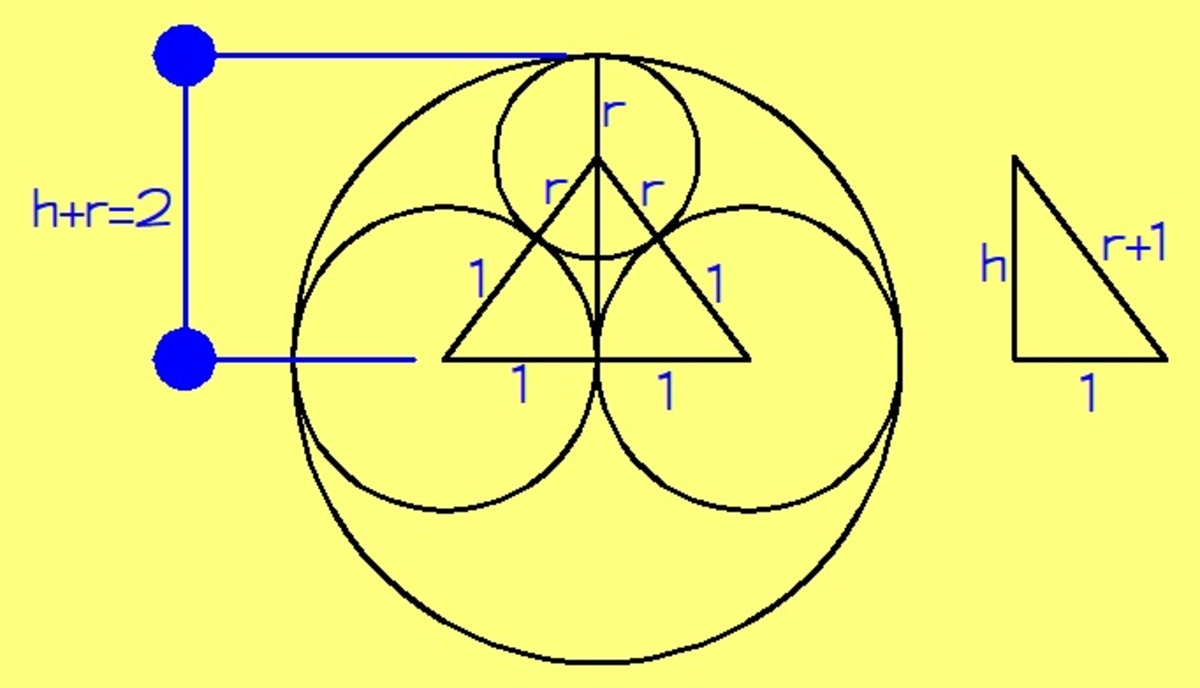By pythagorean theorem, we have

( r + 1 ) 2 = h 2 + 1 (r+1)^2=h^2+1

r 2 + 2 r + 1 = h 2 + 1 r^2+2r+1=h^2+1

r 2 + 2 r = h 2 r^2+2r=h^2

h = r 2 + 2 r h=\sqrt{r^2+2r}

Hence,

2 = h + r = r 2 + 2 r + r 2=h+r=\sqrt{r^2+2r}+r

2 − r = r 2 + 2 r 2-r=\sqrt{r^2+2r}

Square both sides.

( 2 − r ) 2 = ( r 2 + 2 r ) 2 (2-r)^2=(\sqrt{r^2+2r})^2

4 − 4 r + r 2 = r 2 + 2 r 4-4r+r^2=r^2+2r

4 = 2 r + 4 r 4=2r+4r

r = 2 3 ≈ 0.66667 r=\dfrac{2}{3}\approx 0.66667

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Akash Singh
Feb 17, 2016

drop perpendicular from O to AB as D

OB = 1+r

DB =1

so find OD

and OD + r=2

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...