Find REMAINDER.

Level pending

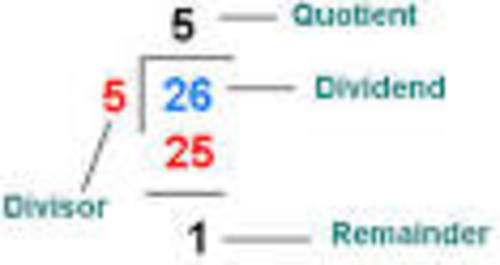Find the remainder when 5^{2009}+13^{2009} is divided by 18.

0 2 1 3

Mayank Devnani by Mayank Devnani , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

General Rule: If (x^m+y^m) is divided by x+y them reminder will always be zero if m is an Odd no. Here, (5^2009 + 13 ^ 2009) /(5+18) and 2009 is odd no, so reminder will be zero.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

If m is an even no. , then ???

Mayank Devnani - 7 years, 4 months ago

Take the lowest index possible as in 5 exp 1 + 13 exp 1 /18 , remainder is null , try next digit with index 2 , as in 5 exp 2 +13 exp 2, remainder is non null , so it seems that it is cyclic about odd indices... which carries a remainder of null.

aritri chatterjee - 7 years, 4 months ago

@Aritri If question says that find remainder and 2009 is replaced by 3000. So what's the answer ????

Mayank Devnani - 7 years, 4 months ago

@Mayank 3000 is supposedly evenly perceived, now if 5 exp 2 +13 exp 2 /18 leaves a remainder of xyz is not important , the point is by mathematical induction all indices in multiples of 2 [ which in this case is 3000] as in 5 exp 3000+13 exp 3000/18 leaves a remainder of 14.

aritri chatterjee - 7 years, 4 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...