Find Squares - Can You Count Them All?
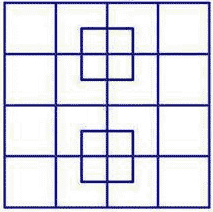How many squares are in this picture?
Details and Assumptions :
Distinct squares can overlap one another.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
i counted the boxes manually :p
Log in to reply
Me too.. sometimes dumbing down the process helps.. especially for folks like me who are bad at formulae! :)
Log in to reply
dont go by formula, go by the process. And in mathematics every formula is generated by a process
So that makes it:
Number of squares in the 4 x 4 square + 2 times (Number of squares in the 2 x 2 square)
= 4 2 + 3 2 + 2 2 + 1 2 + ( 2 × ( 2 2 + 1 2 ))
= 4 0
Damn cool!
Log in to reply
hahahah i just found it after count manually :p
Leave the formula behind !!!! Apply ur own brain dude !!! do u know how the formula above came from ??? ... Just feel the question . _ Ur target is to find total no of squares. What u r supposing or assuming will be totally wrong at a moment.. _ visually based on ur mindset , u will be able to count squares but later seeing options .. u see ur answer is too small. STEP 1 :- Count the biggest square .... yes , a square of 4 blocks is = 1 STEP 2 _:- Count second biggest squares ... yes , squares of 3 blocks... i.e = 4 _ ( see image carefully !! ) Step 3 _:- Count third largest squares... yes, squares of 2 blocks ... i.e = 9 ( again see ... ) _ _ Now u carefully see the observation upto this .... and u see that a Series is FORMING !!!!! Right !! 1= 1^2 , 4 = 2^2 , 9 = 3^3 . _ _ Yes !!! a series of squares of natural number and here natural no. are the no. of blocks consisting in biggest and smallest square. ( excluding the two square in middle ) . Therefore .. total no of square formed till now = 1 +4+9+16 ( 16 is of small squares ) = 30 _ Now Extra SQUARES = 4+4 ( smallest blocks ) + 1+1 ( small blocks ) = 10.
THEREFORE .. FINAL ANSWER IS 40 !!!!!
Log in to reply
I did exactly that but I started with the smallest squares and started moving up in size :D
That way is much easier
It should be 32. Becuase Where there are two squares inside 4X4 squares, the outside of the small squares is not a square shape! So, I think It should be like this 40-8=32. Am I clear?
Log in to reply
the 8 additional squares come from the two 'extra' unaligned squares inside the 4X4 squares. Each 'extra' square was divided into four smaller squares by the 'original' lines in the 4X4 grid
Log in to reply
You are right Mikhaella But My point is the outside area of extra two unaligned squares, there are 8 squares which is not actually is in a shape of square. I mean the 8 squares of column 2 and 3 are not actually squares !!! Am I right?
simply, it is 16 1x1, 9 2x2, 4 3x3, 1 4x4 and 5+5 in the small squares
good explanation
I also just counted them right, no formula :P
Could please provide the derivation of the formula
I have no knowledge of formula ,but its a good explanation.
this is the best solution
40 i counted the boxes manually
nice question
The outside area of the two extra unaligned squares, there are 8 squares which is not actually is in a shape of squares. I mean the 8 squares of column 2 and 3 are not actually squares !!! Am I right? So that should be like this 40-8=32 !!!!!??????
(1^2 +2^2 +3^2 +4^2)+ (4+1)+ (4+1)=40
i did n i found the formula u,u
it was sigma n sqr with............n=4 .......................and the mini squares are also calculated after this
(4)^2 +(3)^2 +(2)^2 +(1)^2 =30 for the 4x4 square & for the two 2x2 squares its : 2( 2^2 + 1^2 ) = 10 and the total is 30 + 10 = 40
Here is the Manual Solution (Not Equation), Just look at the figure while reading each line and you should be able to understand it simply.
There are : Normal squares, that are simply counted, the two in the middle squares, the tiny which are inside the two in the middle, big squares (1 big square = 4 normal squares) , and huge squares (1 huge square = 9 normal squares.) and the whole square
Simply just count the normal squares which are 16 squares,
then there two squares in the middle. that makes them 18
and then the tiny squares inside the two in the middle which are 8 squares, that's a total of 26 then
you will start counting each big squares (4 normal squares) if you have a good vision you will be able to find that if you divide the whole square (The who figure), you might notice that there are 4 big squares that are made of 4 normal squares. (Divide the whole figure into 4),
They might look just as 4 but you forgot the 3 Vertical Big Squares (in the middle) and the other 3 Horizontal squares (in the middle), if you count them well, they should be about 9.
Then from each corner try to make a 3x3 square, you will get 4, now lets add them all
16 normal squares + 8 Tiny squares + 2 the squares in the middle + 9 Big squares + 4 Large squares (3x3 squares) = that's all if you calculate it is equal to 39, oh wait the answer is 40, where is the left one? The Last one is the WHOLE Figure (4x4) which is a square as well so, here are 40 squares.
(This question needs someone who has a good visual discerning and scrutinizing ability or just someone who is really good at making/creating equations.)
40 is right answer
Thanx for the formulae....its very helpful :)
I don't get it by formula neither by counting manually. .. Can anyone tell me how to count manually.
I counted them manually but somehow short of 8.
How come that there are 10 squares added?
At the risk of sounding like an idiot, the answer in 'count the squares, or triangles or whatever' is always the largest answer. Yet to come across a problem where it isn't.
same way like you
even small squares counties 4 thats is mistakes lol
Let’s assume the smallest square side is 0.5cm in length.
Now count the squares with different length :-
0.5cm : 8
1cm : 16 +2(in the middle)
2cm : 9
3cm : 4
4cm : 1
———— Total : 40
Its the sum of first four square numbers. i.e 1^2+2^2+3^2+4^2=30 and 2+2 squares at the middle with 4 enclosed within each= 30+2*4+2=40
I can't see how 92% of people got this wrong. It isn't that hard.
what if there are odd number of squares?
The approach should be correct. Count all the square of each size, one by one. Thus thus correct answer at which you ll come is 40.
you can easily solve it with some good concentration
There does exists a formula for this problem, but here is something that would be simpler in terms of how much easier it is to understand that came into my mind:
Let there exist 3 cases such that individually the cases define the values that when added together we reach our answer.
Case 1.) The largest box is divided up into 4 rows and 4 columns. From this we get: 4 x 4 = 16. We also account for the largest box in its undivided form so: 16 + 1 = 17 Thus: Case 1 = 17
Case 2.) There are two boxes (2) placed on vertical center line (middle) that are both divided up into four boxes (4) so we can get: 2 x 4 = 8 We also account for the two boxes that exist in their undivided form so: 8 + 2 = 10 Thus: Case 2 = 10
Case 3.) Now we can account for the fact that within the 4 x 4 grid of squares made from the largest square, we can have squares that have sizes of 3 x 3 and 2 x 2. There exist four 3 x 3 squares and nine 2 x 2 squares (There is a formula to get this in a quicker way but I will not put it up since it is a bit difficult to explain) so we can get: 4 + 9 = 13. Thus: Case 3 = 13
We add Case 1, Case 2, and Case 3 to get: 17 + 10 + 13 = 40 and we are done.
I will admit that this is not the best solution. Instead, this is a solution that is easy to understand. This solution is literally taking counting each square to the level just above it. Hope this works for you :D
Consider an edge of the square as 1 unit, hence
Nos of 0.5 0.5 squares in the center = 4 2 = 8
Nos of 1 1 squares = 4 4 + 2(The squares inscribed inside) = 16 +2 = 18.
Nos of 2*2 squares = 4(at the edges) + 3(aligned in the center vertically) + 2(aligned in the center horizontally) = 9.
Nos of 3*3 squares = 4(each corner)
Nos of 4*4 squares = 1
Total squares = 8+18+9+4+1 = 40.
excluding the two smaller squares, there are 30 squares in the four by four grid by the sum of squares formula. then, simply add the ten remaining squares generated by the smaller squares to obtain an answer of 40.
I have count them and I found 32 in this picture
Log in to reply
Hi, the inner two squares at the middle have enclosed squares too so you can add additional 8 squares that would give us 40. I just tried to recount it. =)
a) 4 x 4 =1 b) 3 x 3 = 4 c) 2 x 2 = 4 + 5 = 9 d) 1x 1 = 16 + 2 =18 e) 1 x ¼ = 8 Total 40
Wouldn't it be 41? Math aside, nobody seems to be counting the 1 largest square. Correct?
Well there is a formula that check-box of n × n squares, the total no. of squares in it is given by............
n 2 + ( n − 1 ) 2 + ( n − 2 ) 2 . . . . . . 1 2 .
i.e. here in the box of 4 × 4 , the total no. of squares are 4 2 + 3 2 + 2 2 + 1 2
i.e. 3 0
Also there are 2 small squares in middle along with 4 accompanied even smaller squares each. total = 1 0 .
Hecne THE TOTAL COUNT is 3 0 + 1 0 i.e. 4 0
Easy no! :)