Find the Angle #2
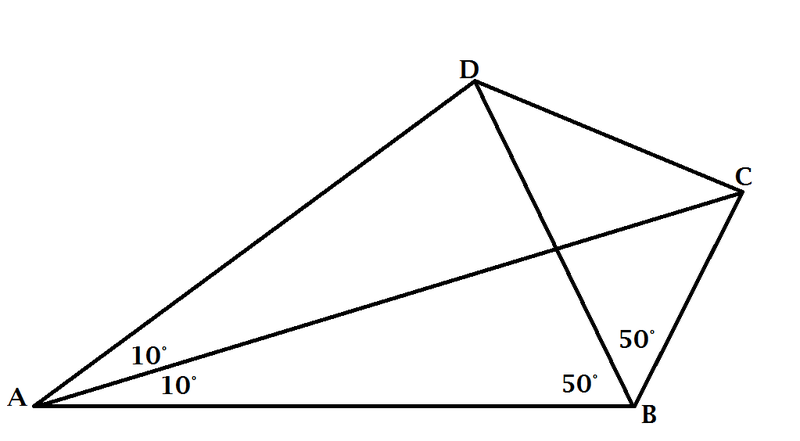 ∠
C
A
D
=
∠
B
A
C
=
1
0
∘
and
∠
D
B
A
=
∠
C
B
D
=
5
0
∘
.
∠
C
A
D
=
∠
B
A
C
=
1
0
∘
and
∠
D
B
A
=
∠
C
B
D
=
5
0
∘
.
Find ∠ B D C .
This problem is a part of the set Find the Angle!
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I used trigonometry here I assumed a side length equal to 12 in AB then continuously used the sine law.
Relevant wiki: Sine Rule (Law of Sines)
Let A C and B D meet at O . Then ∠ A O B = ∠ C O D = 1 8 0 ∘ − 1 0 ∘ − 5 0 ∘ = 1 2 0 ∘ ; ∠ A O D = ∠ B O C = 2 3 6 0 ∘ − 2 4 0 ∘ = 6 0 ∘ ; ∠ O C B = 7 0 ∘ and ∠ A D O = 1 1 0 ∘ .
Let A B = 1 . By sine rule: A B O B = sin ∠ A O B sin ∠ O A B ⟹ O B = sin 1 2 0 ∘ sin 1 0 ∘ × A B = sin 6 0 ∘ sin 1 0 ∘ . By sine rule again: O C = sin ∠ O C B sin ∠ O B C × O B = sin 7 0 ∘ sin 5 0 ∘ × sin 6 0 ∘ sin 1 0 ∘ .
Similarly, A O = sin ∠ A O B sin ∠ A B O × A B = sin 6 0 ∘ sin 5 0 ∘ . And D O = sin ∠ A D O sin ∠ D A O × A O = sin 1 1 0 ∘ sin 1 0 ∘ × sin 6 0 ∘ sin 5 0 ∘ = sin 7 0 ∘ sin 1 0 ∘ × sin 6 0 ∘ sin 5 0 ∘ = O C .
Therefore, △ D O C is isosceles with ∠ C O D = 1 2 0 ∘ , then ∠ B D C = ∠ O D C = ∠ O C D = 2 1 8 0 ∘ − 1 2 0 ∘ = 3 0 ∘ .
Easy way:
Extend A D and B C to meet at E . Since B D and A C are angle bisectors, their intersection (call it I ) must be the incenter of Δ A B E . We also have ∠ A E B = 6 0 ∘ by angle sum of triangle, so ∠ C E I = 3 0 ∘ . Furthermore, ∠ A I B = 1 2 0 ∘ , so ∠ D I C = 1 2 0 ∘ . Thus, we have D I C E is cyclic, since the opposite angles sum to 1 8 0 ∘ . Therefore, ∠ B D C = ∠ I E C = 3 0 ∘ .