Find the angle
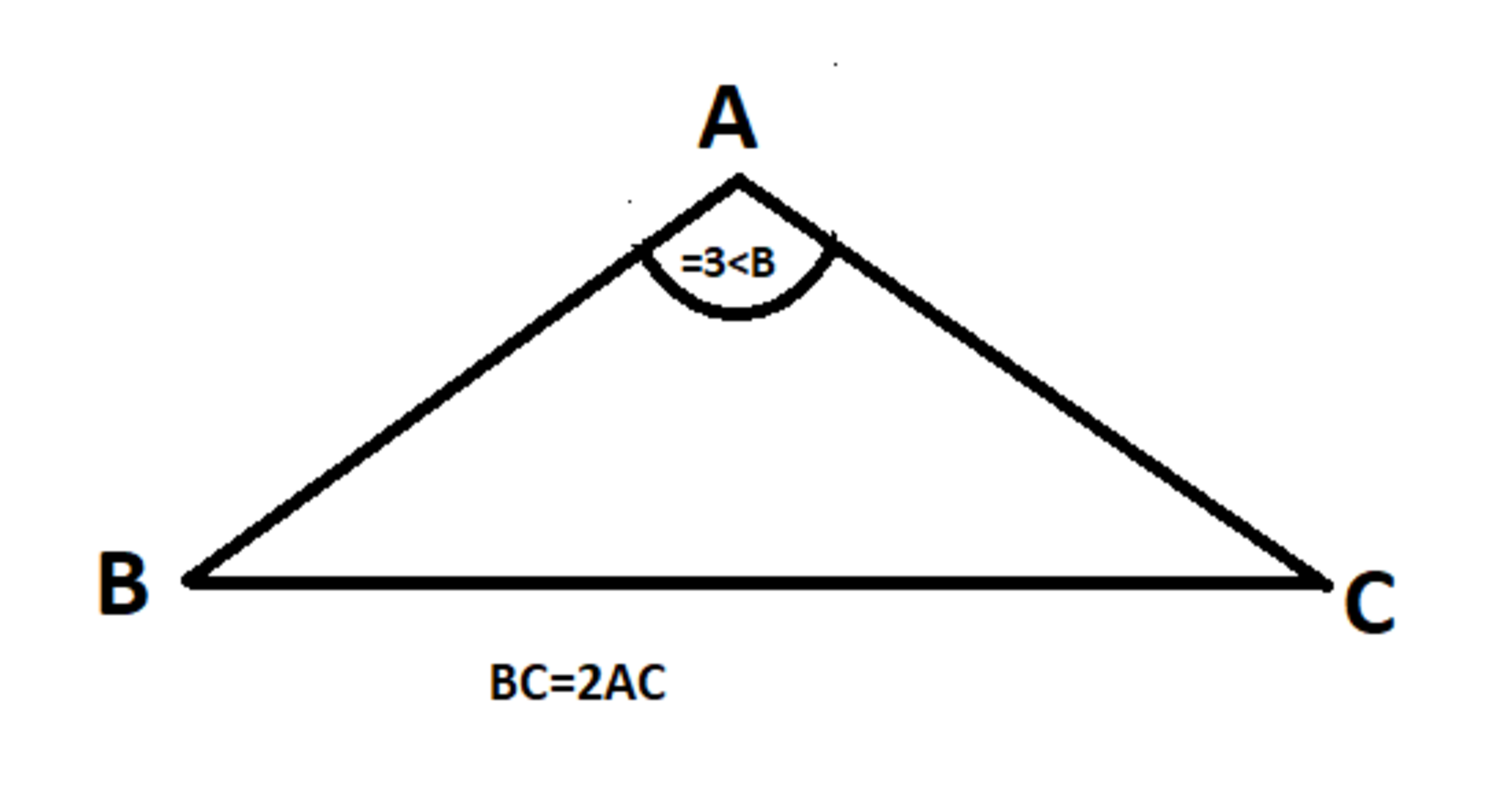
In △ A B C , B C = 2 A C and ∠ A = 3 ∠ B , find the measure of ∠ A in degrees.
Note: The figure is not to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let ∠ B = θ and A C = 1 ; then ∠ A = 3 θ and B C = 2 . Using sine rule ,
B C sin ∠ A 2 sin 3 θ sin 3 θ 3 sin θ − 4 sin 3 θ sin θ − 4 sin 3 θ sin θ ( 1 − 4 sin 2 θ ) = A C sin ∠ B = 1 sin θ = 2 sin θ = 2 sin θ = 0 = 0
⟹ sin θ = 0 ⟹ θ = 0 ∘ ⟹ ∠ A = 3 θ = 0 ∘ Not acceptable
⟹ sin θ = ± 2 1 ⟹ { θ = 3 0 ∘ θ = 1 2 0 ∘ ⟹ ∠ A = 3 θ = 9 0 ∘ ⟹ ∠ A = 3 θ = 3 6 0 ∘ Acceptable Not acceptable
SOLUTION 1: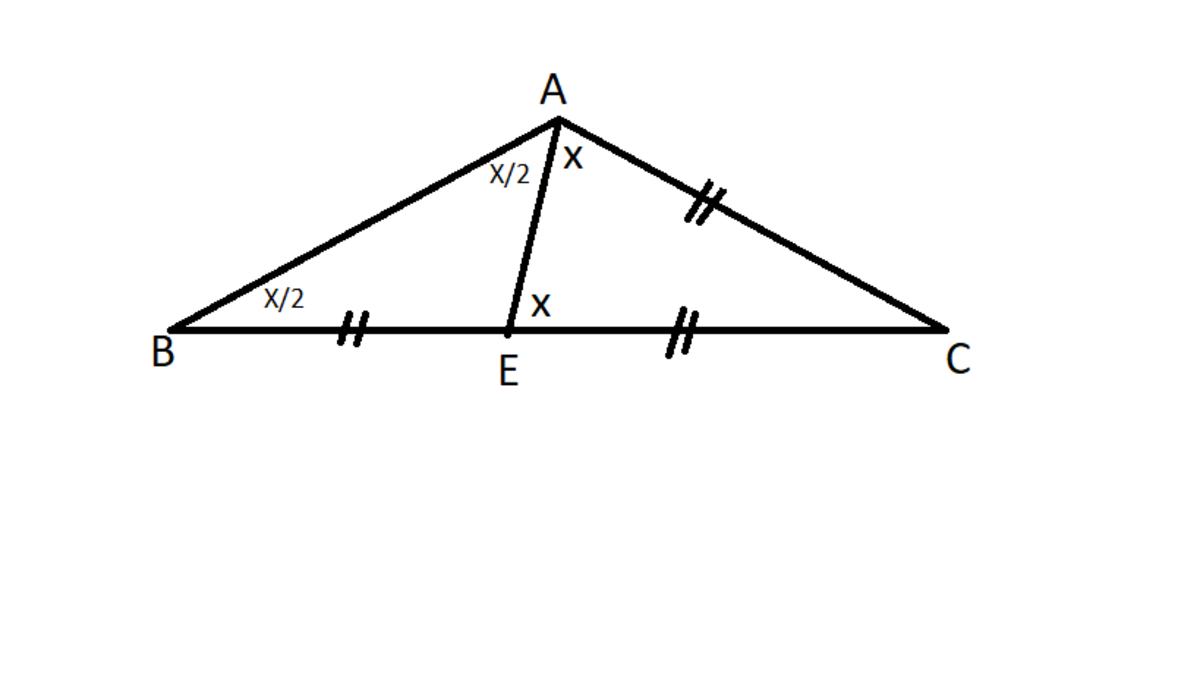 OKAY! the problem may seem easy at first sight , but trust me,it took me 3 hours to reach the solution!!now,lets move towards to the solution.it is given that the segment BC is twice segment AC.let us draw another line(the median) that touches BC at point
OKAY! the problem may seem easy at first sight , but trust me,it took me 3 hours to reach the solution!!now,lets move towards to the solution.it is given that the segment BC is twice segment AC.let us draw another line(the median) that touches BC at point
E.From the picture,it is clear that AC=CE=BE.However.in triangle AEC, AC=CE. thus it is an isosceles,and the shown angles are congruent.Let us determine them as X. angleAEC=X is an exterior angle of triangle AEB. so, ∠X=∠ABE+∠BAE
=∠B+(∠A-∠X)
=∠B+∠A-∠X
=∠B+3∠B-∠X
=4∠B-∠X
so,2∠X=4∠B
or, ∠B= 2 ∠ X . ∠X=∠B+∠BAE
or, ∠X= 2 ∠ X +∠BAE . NOW,∠BAE= 2 ∠ X .SO, AEB is an isosceles.AND,BE=AE=AE=EC=AC.so,triangle AEC is equilateral and ULTIMATELY we find X is equal to 60 degree.BUT,angle A=X+ 2 ∠ X =60+30= 90
SOLUTION 2(ALTERNATIVE): Simply apply sine law ,
s i n C A B = s i n A B C = s i n B A C
Taking last two ratios,
s i n B s i n A = B C A C =2
=>sin3B=2sinB
=>3sinB-4(sinB)^3=2sinB
=>3-4(sinB)^2=2 [dividing both sides by sinB, as sinB≠ 0]
=>(sinB)^2=1/4
=>sinB=1/2=sin30
so, ∠B=30
so, ∠A=3∠B=3x30=90 degree.