Find the angle!

Geometry Level 3

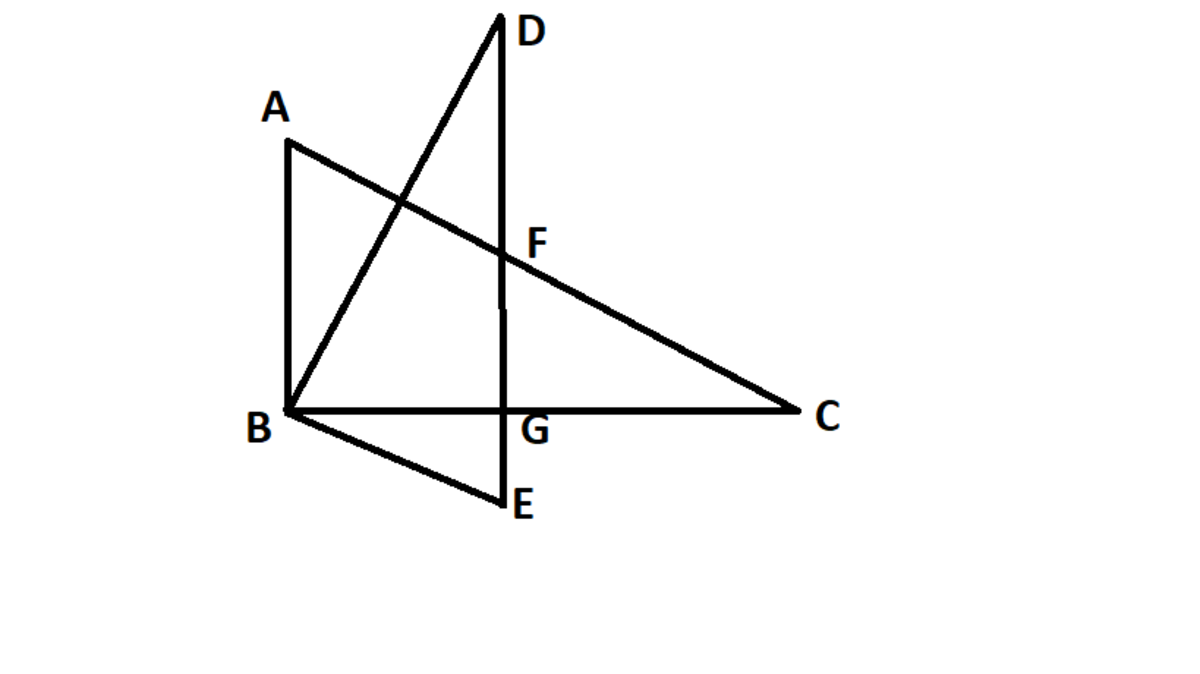In the given diagram,both ABC and DBE are right triangles,B being the right angle for both.They have hypotenuses of same length where F is the midpoint for both.DE is perpendicular on BC.If,the area of ABC is √3 times of DEB,Find ∠BDE.
[figure not drawn to scale]

20 25 15 35

1 solution

Shamin Yeaser
Oct 7, 2017

Since,the both triangles have same length hypotenuses with the midpoint F,the both belong to a same circumcircle with the center F.Its is clear from the picture that,BC has been bisected at point G.Let's consider BG=GC=x and AC=DE=y
According to the question, $\frac{1}{2}$ sinθ.2x.y= $\frac{ √3}{2}$ .y.x
thus, sinθ= $\frac{ √3}{2}$ =sin60°. So,θ=∠ACB=60°
NOW ∠AFD=30°. from the picture, ▲AFD is an isosceles.so,∠ADF= $\frac{180-30}{2}$ °=75°
we also know, ∠ADB=60° [because,∠ADB=∠ACB as the both lie on the same chord]
Finally, ∠BDE=∠ADF-∠ADB=75°-60°=15°

If you don't mind,please check my NOTE called LETS SOLVE TOGETHER.I truly need your help!! I would appreciate if you guys help me finding out the solution! thank you

Area of abc=root3 times of which triangle... Def are collinear naa

rakesh chitrada - 3 years, 8 months ago

I apologize,it was completely my mistake.I am sorry,please.Now I have corrected that.I would be happy if you try to solve it now and also help me with the NOTE!

Shamin Yeaser - 3 years, 8 months ago

Find the angle!

1 solution

0 pending reports