Do The Angle Chasing Dance
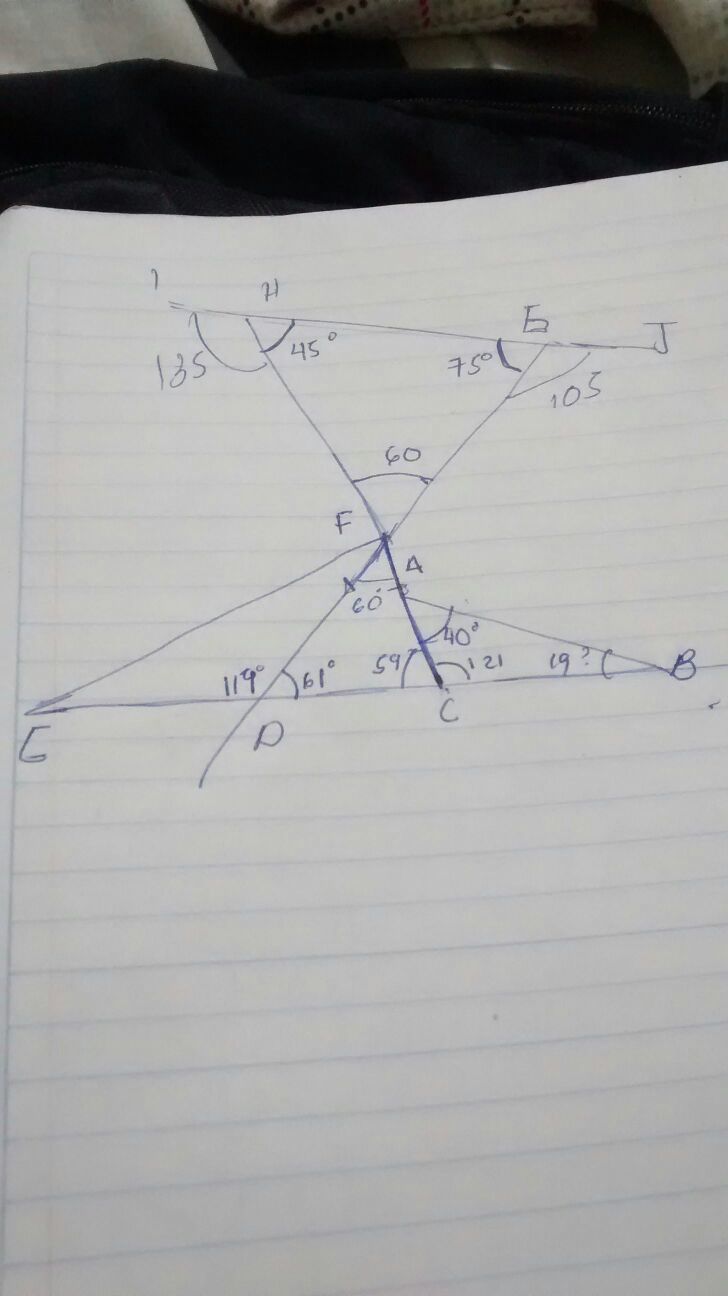
In the figure, with ∠ B A C = 4 0 ∘ , what is the measure of ∠ A B C (in degrees)?
Clarification:
H
F
A
C
,
D
F
G
,
E
D
C
B
,
I
H
G
J
are all straight lines.
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
26 solutions
Beautifully explained without specific working.
Good job, Sarapee.
Really amazing work done!
Great dance move! :) Nicely explained!
I was really confused and just randomly decided to find the degrees for the other triangles as a last hope. Good thing for me it was the solution
Arrows do not show what numbers are used to find the angles they point to.
You could yet to 60 then use the 119 with exterior angles of a triangle are equal to the sum of the two opposite interior angles to get the 121
∠FHG =( 180° - ∠FHI ) = ( 180° - 135° ) = 45° So, ∠GFH = ( ∠FGJ - ∠FHG ) = ( 105° - 45° ) = 60° And ∠ DFC = ∠ GFH = 60° So, ∠FCD = ( ∠EDF - ∠DFC ) = ( 119° - 60° ) = 59°
So, ∠ACB = 180° - ∠FCD = 180° - 59° = 121°
So, ∠ABC = 180° - ( ∠ACB + ∠BAC ) = 180° - ( 121° + 40° ) = 19°
So, ∠ABC = 19°.
Well explained.
Can you please explain what angle chasing is? I solved this problem, but not using that method
Log in to reply
sorry, I gave this problem's title as "Find the Angle" .. but the Brilliant.org admins changed the title and made it "Do The Angle Chasing Dance" ^_^
Angle chasing basically means that you find the measure of several angles, using basic relation (like the sum of angles in a triangle). You are 'chasing' down the value, hence the name.
∠FHI=135° ∠FHG =(180°-∠ FHI ) =46° ∠FGJ=105° ∠FGH=180°-105°=75° WHOLE ANGLE OF TRIANGLE SUM IS 180°. AS SOO NO ANSWER IS 19
180-135 is not equal to 46
beautyfully explained.
In the figure, angleJGD and angleEDG are alternate angles. But the difference between the 2 angles is 14 because segment IJ is not parallel to segment EB.
Therefore, we substract 14 from 135 degrees inorder to get angleACB. Which is equal to ( 135 - 14 = 121 )
The sum of all angles of a triangle is always 180 degrees.
Let angleABC = X
40+121+X=180
161+X=180
180-161=X
X=19
How the difference of 14 is calculated
can u tell what makes u assume the logic of lines will become parallel.......... support you justification with some theorem or lemma or proof
From collrelation of different angles,we get < FCD as 59 degree so ,ACB is 121 and therefore <ABC will be 180 -(40+121) = 19 degree ans. K.K.GARG,India
But instead of saying "JGD and EDG are alternate angles" you should have put it like "if they were to be alternate angles", coz alternate angles occur in || lines only
Nice problem Easy but need to be awake to triangle old rules :-)
This is a really clever(different; If I may) approach. Thanks :)
dear frnds where you see 121 degree angle,there is 119 degree angle.
Log in to reply
Hey you dumb, 121 degree is angle ACB whereas 119 degree is angle EDF.
Nice
find the FED?
find all the angles in this order n then you'll get ABC. GHF, HGF, HFG, DFC, FDC, FCD, then ABC= FCD - CAB
I like this one. :)
Brilliant!
That's exactly how I did it too!
(linear pair) <IHF + <FHG = 180, 135 + <FHG = 180, <FHG = 180 - 135, <FHG = 45 (linear pair) <JGF + <FGH = 180, 105 + <FGH = 180, <FGH = 180 - 105, FGH = 75 (sum of angles in the triangle)<FHG + <FGH + <GFH = 180, 45 + 75 + <GFH = 180, <GFH = 180 - 120, <GFH = 60 (vertical angle) <DFC = <GFH, <DFC = 60 (linear pair) <EDF + <FDC = 180, 119 + <FDC = 180, <FDC = 180- 119, <FDC = 61 (sum of angles in the triangle) <EDF + <FDC + <FCD= 180, 60 + 61 + <FCD= 180, <FCD = 180-121 <FCD = 59 (linear pair) <FCD + <ACB = 180, 59 + <ACB = 180, <ACB = 180-59, <ACB = 121 (sum of angles in the triangle) <ACB + <CAB + <ABC= 180, 121 + 40 + <ABC= 180, <ABC= 180-161, <ABC= 19
as the figure reflects <h= 180-135=> 45 : <g=180-105=> 75: by these two <hfg=>60: by this we can easily get triangle FDC is equilateral and <ACB as 180-60=> 120 and <CBA= 180-(120+40)=> 20. Thanks ..
i gave the answer 20 silly calculation error PHEW.....
∠HFG = ∠DFC = 180 - (45 + 75) = 60
∠CAB + ∠ABC = ∠FCD
40 + ∠ABC = 180 - 60 - 61
∠ABC = 19
∠CAB + ∠ABC = 180 - ∠FCD
As <JGF=105, so, <HGF=180-105= 75 Again, as <IHF=135, so, <GHF=180-135= 45 So, <GFH= 180-45-75= 60 Again, <CFD=<GFH= 60 As, <EDF=119, so, <CDF=180-119= 61 So, ACD=<FCD=180-60-61=59 So, <ACB=180-59= 121 So, <ABC=180-121-40= 19 So, answer: <ABC= 19...
It's very easy question .. 👍
All depends on straight line is 180 and the total of the triangle angles is 180. Result is 19.
Mr. Aashutosh anand..... Very nice question.....
Easiest question posted on brilliant
you say that all the time bro , great.
Given:- <IHG=135°, <FGJ=105°, <FDE=119°, <BAC=40°
To Find:- <ABC
Solution:-
1) In triangle HGF,
a) <GHF=180°-<IHF=180°-135°=45° <GHF=45°
b) <HGF=180°-<JGF=180°-105°=75° <HGF=75°
c) <HFG=180°-(<GHF-<HGF)=180°-(75°-45°)=180°-120°=60° <HFG=60°
2) <HFG=<DFC {Vertically Opposite Angles} <DFC=60°
3) <FDC=180°-<FDE=180°-119°=61° <FDC=61° {Linear Pair of Angles}
4) In triangle FDC, a) <ACB=<FDC+<CFD=60°+61°=121° <ACB=121° {Sum of two opposite interior angles is equal to the sum of the exterior angle}
5) In triangle ABC, a) <ABC=180°-(<ACB+<BAC)=180°-(121°+40°)=180°-161°=19°
Therefore, the measure of <ABC=19°
FHG = 180 - 135 = 45
FGH = 180 - 105 = 75
HFG = 180 - (45 + 75) = 60
DFC = 60
FCD = 119 - 60 = 59
ACB = 180 - 59 = 121
ABC = 180 - (121 + 40) = 19
in the Figure Angle 180-105=75, 180-135=45, So angle at F is 60 Angle At D is 180-119=61, Angle at ACD is 59 and Angle at ACB=121 angle at B is 19
According to the picture above, what is the measure angle ABC (in degrees) of ?
Clarification: are all straight lines.
Solution angle HGF = 75, a, angle GHF = 45, angle HFG = 180 – 75 – 45 = 60
Now angle DFC = 60 opposite angles at a F.
Consider triangle DFC angle EDF is external angle EDF = angle DFC + angle DCF There fore angle DFC = 119 – 60 = 59
And this is external for triangle ABC therefore angle B = 59 – 40 = 19
Trivial:
FHG is 45, FGH is 75. HFG and DFC are 60, then FDC is 61 and DCF is 59. ACB is 121, and if we know that CAB is 40 then CBA is 180-161=19.
Every single triad of letters is obviously an angle.
Note: I hate solutions written like that, but it's a lazy moment.
Firstly ,angle FHG +180-135=45degree then angle.HGF +180-105=75degree then by Angle Sum Property{ASP} of triangle angleHFG = 180-120=60degree . now angleDFC=angleHFG=60 degree.{vertically opposite angles} angleFDC=180-119=61degree so by ASP again,angleFCD=180-121=59degree now ,angle ACB=180-59=121 degree now to get angle ABC we apply ASP again therefore angleABC=180-40+121=19degree
HENCE......its solved.
GHF-45 HGF-75 HFG-60 GFC-120 DAC-60 ADC-61 ACD-59 ABC-19
Using alternate interior angles, you follow your way to the needed angle.
Using 3 simple equations:
180-((180-135)+(180-105))=60 HFG
180-((180-119)+60)=59 ACD
180-((180-59)+40)=19 ABC
40+121+X=180
161+X=180
180-161=X
X=19
consider in triangle FCD
angle FCD = 40 + x angle DFC = 180 - angle HFG= 180 - ( 180-135) + ( 180 -105 ) = 180 - 45+75 = 180 - 120= 60 angle FDC = 180-119=61
so.... angle DFC + FCD + CDF = 180 60 + 40 + x +61 = 180 x = 19 degree hence done :P
From Given angles in figure,taking adjacent angles calculations as 180- given angles, we get<CDF=61,<FGH =75,<FHG=45 so <GFH =60 gegree,and >CFG =60( opposite angles Now from triangle CDF we get DCF =59 degree and slo angle BCA = 121. Since <BAC =40 ( given) therefore anfgle CBA = 180 - (40 +121)= 19 degree Ans K.K.GARG,India
In the figure, angleJGD and angleEDG are alternate angles. But the difference between the 2
angles is 14 because segment IJ is not parallel to segment EB.
Therefore, we substract 14 from 135 degrees inorder to get angleACB. Which is equal to ( 135 - 14 =121)
The sum of all angles of a triangle is always 180 degrees.
59=40+x
x=19
Find Angle GHF & HGF. by this we can find angle HFG . Angle HFG= Angle DFC. In triangle Def, let angle def = x, then 119+ x + x =180 , x = 30.5 Then Angle FEC + Angle EFC = Angle FCB = 60+30.5+30.5 = 121 In triangle ACB, let let Angle ABC = y. Then 121 + 40 + y =180. y = 19. Hence solved
In triangle HGF
180-135 = 45 < its angle H and 180-105 = 75...... Angles on the straight line
then angle F = 60 sum of angles in the triangle
In triangle CDF : Angle F = 60..... opposite angles.
180-119 = 61 which is Angle D in CDF.... angles on the straight line.
then 60+61 = 121 which is angle C in ABC. ... exterior angle.
180-40-121 = 19 ... Sum of angles in triangle ABC..
40+121+X=180
161+X=180
180-161=X
X=19
In the figure, I first found the angle measures of triangle FGH which are 45, 75, and 60. Angle HFG is 60 degrees and is a vertical angle with angle DAC so angle DAc is equal to 60. next you find the rest of the angle measure for triangle ADC. By doing this you find out that the anlge ACD is eaual to 59 and get that angle ACB is equal to 121. Then you do 180 minus 121 and 40 to get 19 degrees as the measurement for angle ABC
180-135=45,180-105=75,180-(45+75)=60,120-119=61,180-121=59,180-59=121,180-(121+40)=19.
FGH=75,FHG=45=>HFG=60 =>DFC=60(opposite angles)
FDC=61
=>DCF=59
Now,DCF=CAB+ABC =>ABC=19
The Angle Chasing Dance