Find the angle;}
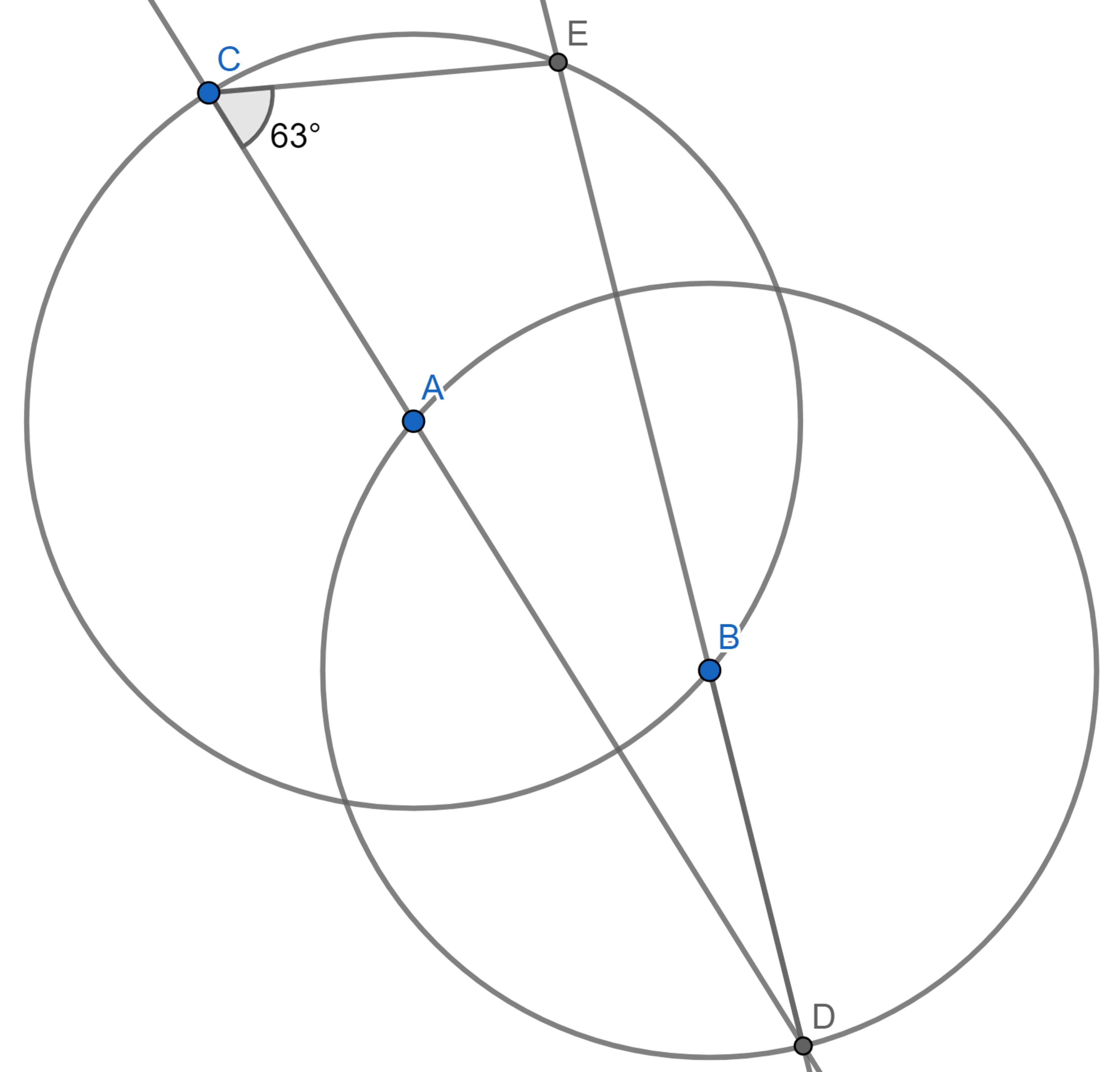 There are two circles of equal size, with their centers
and
on each other's edge. The points
and
are placed on the circle with center
, and the point
is placed on the circle with center
, such that
lies on
, and
lies on
. What is angle
, if
?
There are two circles of equal size, with their centers
and
on each other's edge. The points
and
are placed on the circle with center
, and the point
is placed on the circle with center
, such that
lies on
, and
lies on
. What is angle
, if
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 3 ∘ + 6 3 ∘ + x + 2 x = 1 8 0 ∘
3 x = 5 4 ∘
x = 1 8 ∘
And therefore ∠ C D E = 1 8 ∘ .