Find the Angle #4
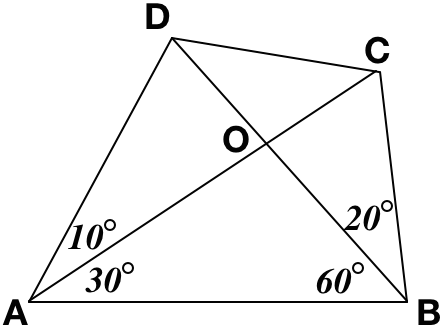 In the above figure,
∠
C
A
D
=
1
0
∘
,
∠
B
A
C
=
3
0
∘
,
∠
D
B
A
=
6
0
∘
,
and
∠
C
B
D
=
2
0
∘
. What is the measure of angle
∠
B
D
C
in degrees?
In the above figure,
∠
C
A
D
=
1
0
∘
,
∠
B
A
C
=
3
0
∘
,
∠
D
B
A
=
6
0
∘
,
and
∠
C
B
D
=
2
0
∘
. What is the measure of angle
∠
B
D
C
in degrees?
This problem is a part of the set Find the Angle!
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Nice. I took a similar approach but ended up with the equation cot ( θ ) = tan ( 3 0 ) tan ( 7 0 ) tan ( 1 0 ) and was wondering how to simplify this (without using a calculator) before writing up a solution, (no reason for that now).
Apparently this type of quadrilateral is called an orthodiagonal quadrilateral . I searched through this link for a more elegant approach to this particular problem and came up empty. However, I learned a few things along the way. :)
Log in to reply
I was also reading up on orthodiagonal quadrilaterals, hoping for a "silver bullet", but finding none.
Looks like we solved the problem in exactly the same way. I trust that somebody will come up with something better, though...
Log in to reply
Yes, I reshared this question in hopes that someone else might know of a "silver bullet". There's no guarantee that there is one, though, and besides, your approach "does the job" just fine. :)
tan ( x ) tan ( 6 0 ∘ − x ) tan ( 6 0 ∘ + x ) = tan ( 3 x ) , set x = 1 0 ∘ , you get your answer.
Log in to reply
Arghh... Why do I keep forgetting about that identity? Anyway, thanks for reminding me. :)
Hello Otto, could you please explain why this cannot be solved using simpler geometry. I mean to say using angle sum properties?
That's my solution. I don't think it's the best, but I liked it. Thank you for share this beautiful problem.
 page1
page1
 page2
page2
 page3
page3
Good job! You have a lot going on with all those variables, but you pull it together nicely at the end.
Nice! You made it well!
Let x = ∠ B D C . Using Law of Sines on:
△ B C D : C D B C = sin 2 0 sin x ; ( 1 ) △ A C D : A C C D = sin ( x + 8 0 ) sin 1 0 ; ( 2 ) △ A C B : A C B C = sin 8 0 sin 3 0 . ( 3 ) Dividing (3) by (2) and using (1), yields sin 1 0 sin 8 0 sin 3 0 sin ( x + 8 0 ) = sin 2 0 sin x , sin x sin ( x + 8 0 ) = sin 2 0 sin 3 0 sin 1 0 sin 8 0 = 2 sin 1 0 cos 1 0 sin 3 0 sin 1 0 cos 1 0 = 1 . Angle x is acute (right triangle ODC), then ∠ B D C = 5 0 ∘ .
A n g l e s a t O a r e c l e a r l y 9 0 o s . L e t x = ∠ B D C . I n Δ D A O , O D A O = C o t 1 0 . I n Δ O A B , A O O B = T a n 3 0 . ⟹ O D O B = T a n 8 0 ∗ T a n 3 0 . . . . . . . . . . ( ∗ ∗ ) I n Δ D A O , O D C O = T a n ( x ) . I n Δ O A B , C O O B = C o t 2 0 . ⟹ O D O B = T a n ( x ) ∗ T a n 7 0 . . . . . . . . . . ( ∗ ∗ ∗ ) B y ( ∗ ∗ ) a n d ( ∗ ∗ ∗ ) T a n ( x ) = T a n 7 0 T a n 8 0 ∗ T a n 3 0 . ∴ x = ∠ B D C = T a n − 1 T a n 7 0 T a n 8 0 ∗ T a n 3 0 = 5 0 o .
i reflected the entire figure across BC, then extended the 2 AD segments so they'd meet and the entire figure becomes a kite.
then i first assumed that all the angles with vertex C are vertical angles, and filled out all the unknown ones, thinking that if they were not vertical angles, then at least 1 triangle would not add up to 180. turns out there was no such mistake. and eventually angle BDC is 50 degrees.
I also solved it using trigonometry (and a calculator) I tried to solve it geometrically as follows: I constructed <bde =,<bca =70 with e on ac so bcde are concylic Now if we can show that be =bd we are done but this is where I am stuck Maybe somebody can finish it from here
This is probably not the most elegant solution, but it gets the job done.
First observe that we have four right angles at O since ABO is a 30-60-90 triangle.
For convenience , we let O B = 1 ; then O A = tan 6 0 (all angles will be measured in degrees). Now O D = ( tan 1 0 ) ( tan 6 0 ) and O C = tan 2 0 . If θ is the angle BDC, then tan θ = O D O C = ( tan 1 0 ) ( tan 6 0 ) tan 2 0 .
I remember a fun fact I learned in school long ago: ( tan 2 0 ) ( tan 4 0 ) ( tan 8 0 ) = tan 6 0 , which follows from ∏ k = 1 ( n − 1 ) / 2 tan ( n k π ) = n for odd n , with n = 9 .
Keeping in mind that ( tan t ) ( tan ( 9 0 − t ) ) = 1 , we find that tan θ = tan 4 0 1 = tan 5 0 and θ = 5 0 o .