Find The Angle

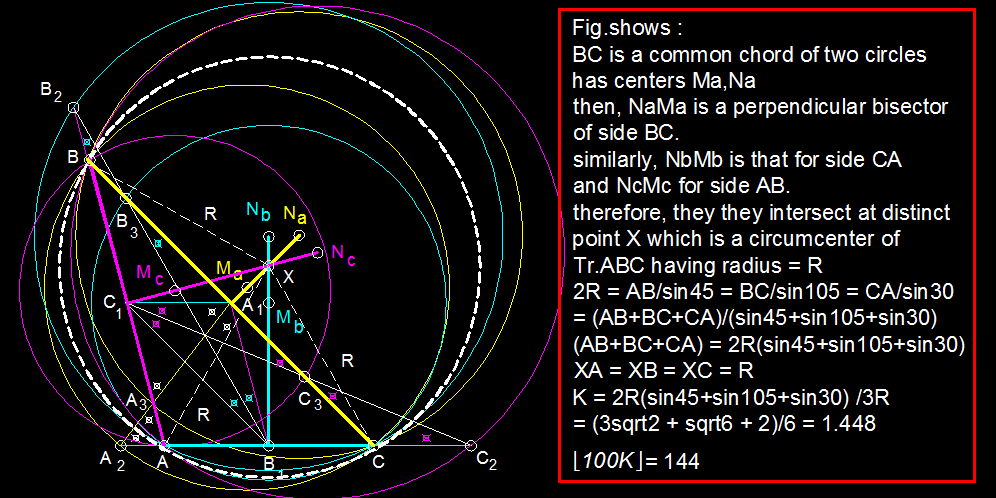
Let $\triangle ABC$ be an acute angled triangle. Let $A_1, B_1, C_1$ be the midpoints of $BC,CA,AB$ respectively. The internal angle bisector of $\angle C_1A_1B_1$ intersects lines $AB$ and $AC$ at points $A_2, A_3$ respectively. Let $M_A$ and $N_A$ be the circumcenters of $\triangle BCA_2$ and $\triangle BCA_3$ respectively. Points $M_B, N_B, M_C, N_C$ are defined analogously. It turns out that lines $M_AN_A, M_BN_B, M_CN_C$ are concurrent at a point $X$ within $\triangle ABC.$ Given that $\angle ABC = 30^{\circ}, \angle BCA= 45^{\circ}$ and $k=\dfrac{AB+BC+CA}{XA+XB+XC},$ find $\left \lfloor 100 k \right \rfloor.$

Details and assumptions
- The floor function $\left \lfloor x \right \rfloor$ denotes the largest integer $\leq x.$ For example, $\left \lfloor 4.3 \right \rfloor = 4, \left \lfloor \pi \right \rfloor= 3.$
- You might use a scientific calculator.
- A picture will accompany soon.
- GeoGebra users will be prosecuted.