Find the angle (for beginners)
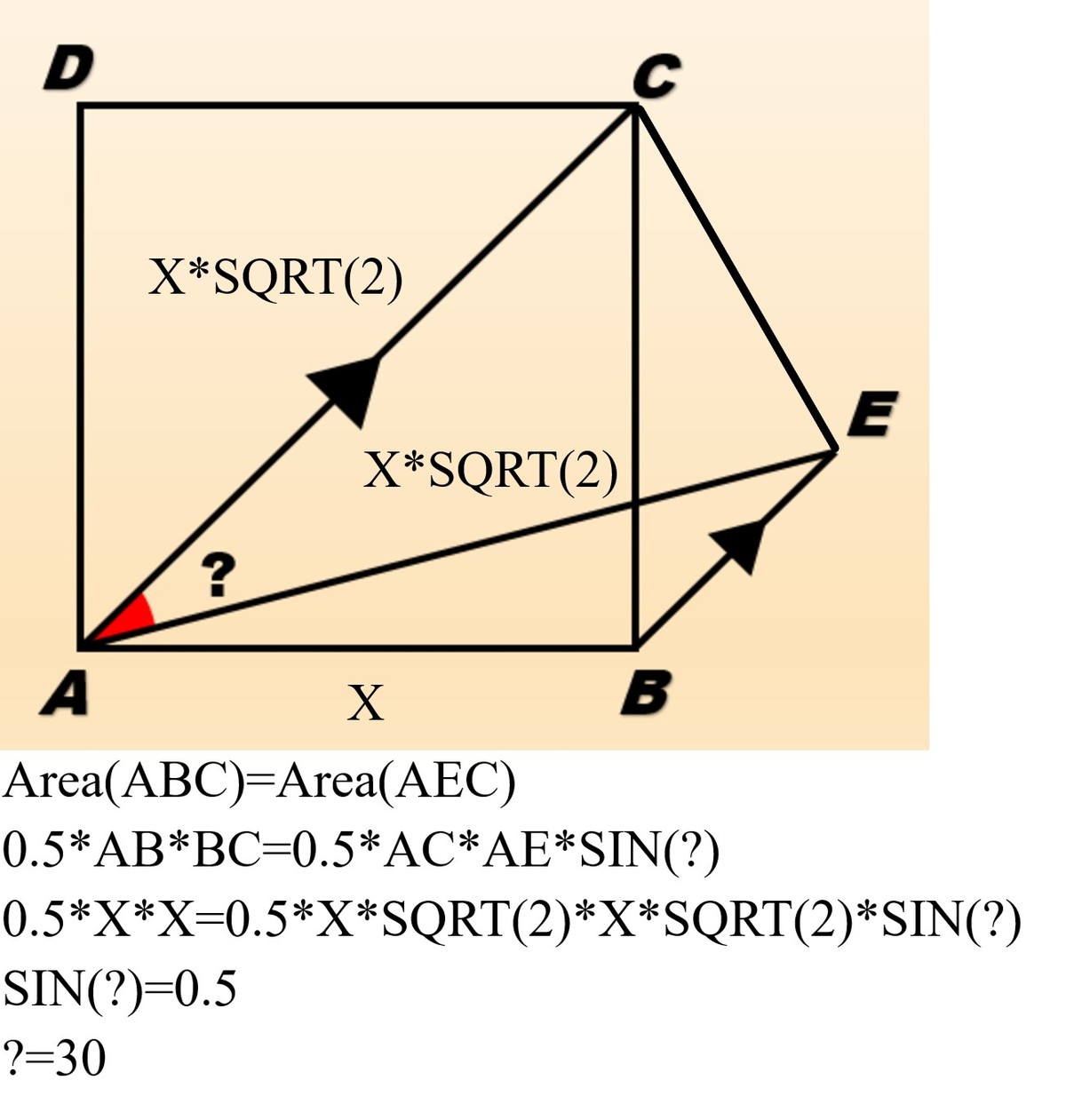
A B C D is a square. A C = A E and A C / / B E .
Find the ∠ C A E .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Just Brilliant!! What was the motivation to reflect the triangle?
@Chan Lye Lee Nice application of "transformation geometry (translational reflection)", likewise approach... cheers!
Let ∣ A B ∣ = x and ∠ E A B = α . Then applying sine rule to △ A B E we get
sin 4 5 ° x 2 = sin ( 4 5 ° − α ) x
⟹ sin ( 4 5 ° − α ) = 2 1 = sin 3 0 °
⟹ ∠ C A E = 4 5 ° − α = 3 0 ° .
Good trigonometric approach!
∠ A B E = 9 0 + 4 5 = 1 3 5 ∘
Let A B = 1 , then A C = A E = 2
Apply sine law on △ A B E
1 sin ∠ A E B = 2 sin ∠ A B E
∠ A E B = 3 0 ∘
It follows that
∠ E A B = 1 8 0 − 1 3 5 − 3 0 = 1 5 ∘
Finally
x = 4 5 − 1 5 = 3 0 ∘
Reflect the triangle A B E over the line B E to get the triangle A ’ B E .
Note that ∠ A B E = ∠ A ′ B E = 1 3 5 ∘ . The ∠ A B A ′ = 9 0 ∘ and hence A A ′ = A C = A E = A ′ E .
The triangle A A ’ E is equilateral. Now ∠ E A A ′ = 6 0 ∘ . Since ∠ B A A ′ = 4 5 ∘ , ∠ E A B = 1 5 ∘ , we have ∠ C A E = 3 0 ∘ .
There are different approaches and discussion in this video .