This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I don't understand how angle CAD and ADB are equal. Can you please explain this part.
Log in to reply
You can easily get ∣ A C ∣ = 2 ∣ A D ∣ cos 3 5 ° . Apply sine rule to △ B A D to obtain ∣ A B ∣ = ∣ A D ∣ × sin ∠ A B D sin ∠ A D B , with ∠ A D B = 6 0 ° + x , ∠ A B D = 5 5 ° − x . Applying sine rule to △ A B C you get ∣ A B ∣ = ∣ A C ∣ × sin 5 5 ° sin 9 5 ° . Comparing the two expressions for ∣ A B ∣ you can get 5 5 ° − x = 3 0 ° .
How do you know that triangle A B C and triangle B C D are isosceles?
Log in to reply
Because ∠ D B C = 2 5 ° ⟹ ∠ B D C = 5 0 ° − 2 5 ° = 2 5 ° .
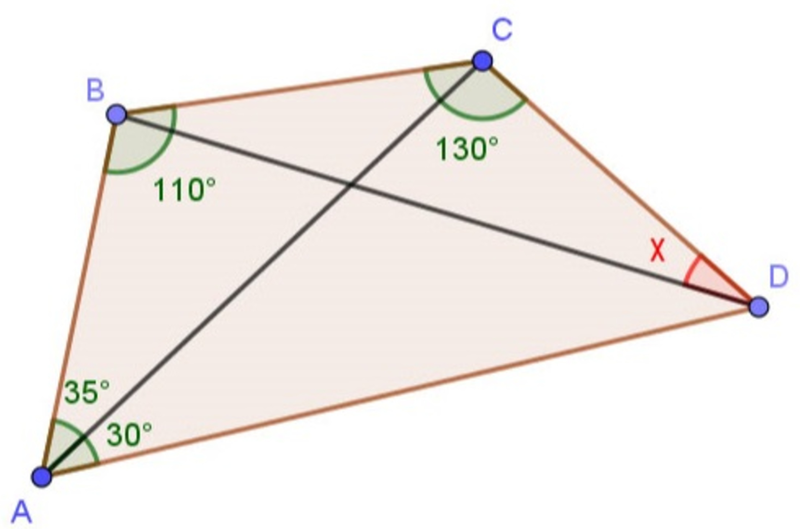
∠ A D C = 5 5 ° , ∠ B C A = ∠ B A C = 3 5 ° , ∠ C A D = ∠ A D B = 3 0 ° . Therefore ∠ B D C = ∠ A D C − ∠ A D B = 5 5 ° − 3 0 ° = 2 5 ° ( △ A B C , △ B C D are isosceles triangles).